The two elastic contact bodies Ω 1 and Ω 2 are separated into two independent objects. According to the elastic finite element theory, their respective finite element basic equations can be written, that is:

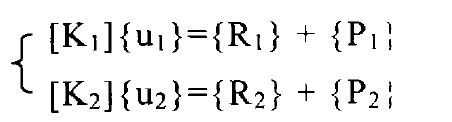
Of which:

[K1], [K2] – stiffness matrix of elastomer Ω 1 and Ω 2;

{U1}, {U2} – node displacement vector of elastomer Ω 1 and Ω 2;

{R1}, {R2} – contact internal force vector;

{P1}, {P2} – load vector.

The formula alone cannot be solved. If {R1}, {R2} is known, the formula can be solved according to the displacement method of finite element to obtain the displacement of nodes. Therefore, it is necessary to obtain the contact internal force vectors {R1}, {R2} according to the contact conditions of contact points.

Let the contact point pairs of Ω 1 and Ω 2 on the contact surface be I (1) and I (2), I = 1,2,3… N respectively. As long as [K1] and [K2] of the formula are nonsingular, the flexibility equation of the contact point pair can be obtained as follows:

Of which:

i. J, K – node number;

I = 1,2,3…. n – logarithm of possible contact points;

N (1), n (2) – the number of external forces acting on Ω 1 and Ω 2;

{pK (1)}, {pK (2)} – outward force acted by node K;

[CIJ (1)], [CIJ (2)] – respectively represent the flexibility value of point I caused by the unit force of point J on Ω 1 and Ω 2