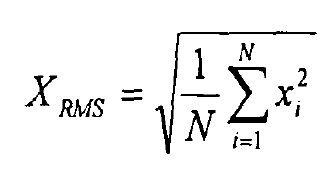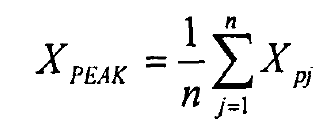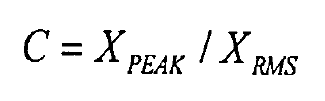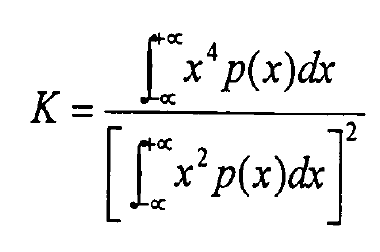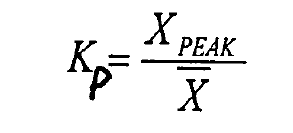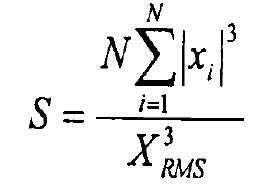In the vibration characteristic analysis of condition monitoring and fault diagnosis, the characteristic parameter method plays an important role. The advantage of characteristic parameter method is that only a few indexes can explain the state of diagnostic object, and the analysis is simple and convenient.
The commonly used characteristic parameters include various amplitude domain diagnostic parameters such as RMS and peak value, and various frequency domain diagnostic parameters such as barycenter frequency.
1) Amplitude domain diagnostic parameters
a. Root mean square value
The root mean square value is defined as follows:
Where {Xi} is the collected signal, I = 1-N, and N is the number of sampling points.
The root mean square value is the average of the signal, so it can give a good evaluation of irregular vibration waveform abnormalities such as surface wear. However, it is not suitable for anomalies with shock vibration. The reason is that the amplitude of the shock wave peak is large, but the duration is short. If the time is averaged, the difference of the peak can hardly be shown.
b. Peak
The peak value is the maximum value reflecting the vibration at a certain time. Assuming that n peaks {xpj} (J = 1-N) have been found from n values of {Xi} by using a peak counting method, the peak index is:
The most commonly used stiffness indexes for amplitude range processing of vibration signals are root mean square value and peak value. The root mean square value and peak value are dimensional parameter indexes. One big disadvantage of using dimensional parameter index to judge fault is that it depends on historical data and is sensitive to the changes of load and speed. In order to overcome this shortcoming, some dimensionless parameter indexes can be used. Common dimensionless parameter indicators include:
c. Peak factor C
d. Kurtosis index k
Where p (x) is the probability density distribution function of X (T).
e. Waveform index KP
f. Skew (skew)
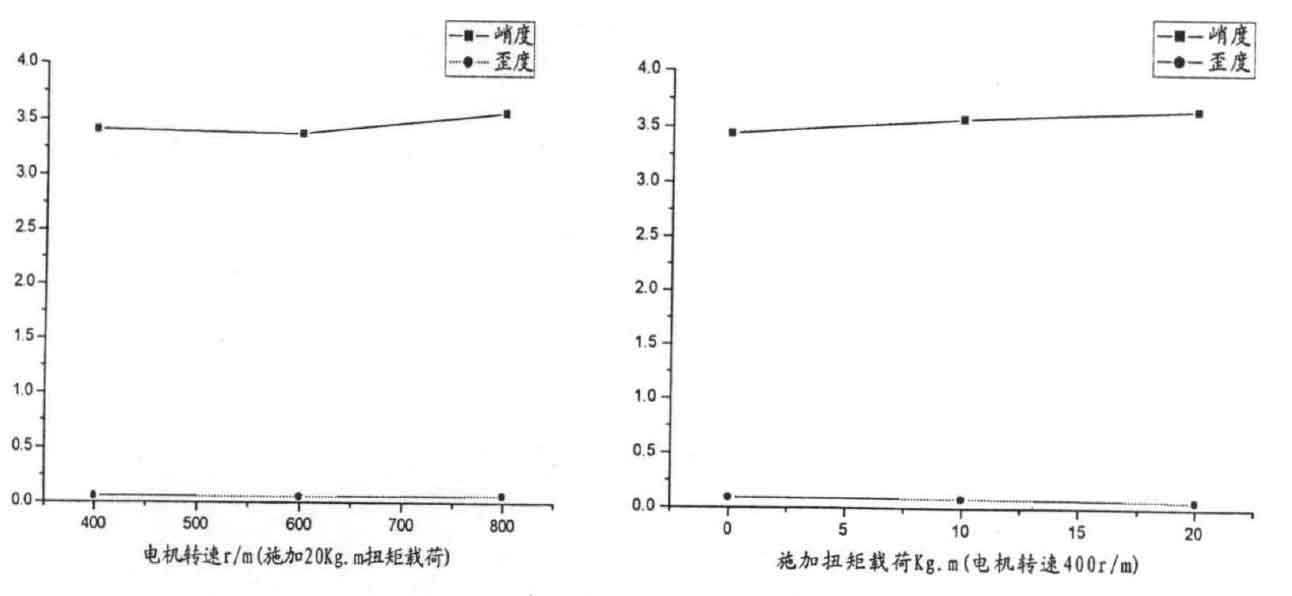
Kurtosis and skewness are two very important dimensionless time domain parameters. When the tractor gearbox works in gear, the kurtosis and skewness values under different states are not sensitive to the change of load. As shown in the figure, it can be seen that the skewness is not sensitive to the changes of speed and load.
We can also see that for the tractor gearbox, the skew value is in normal condition, and in case of local fault, the skew value is, with little change before and after. It can be seen that the skewness value has the characteristics of small variation range compared with other indexes. It can also be seen that the root mean square value, kurtosis and skewness do not change significantly whether the fault occurs or not, and the parameter peak and peak factor change significantly.