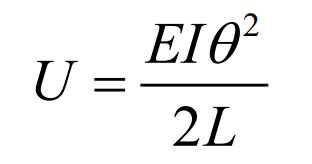The moment of inertia of the section to the neutral axis of the straight bevel gear blank is different in the length direction. The section moment of inertia of the straight bevel gear blank at the cutting position is smaller, and the corresponding stiffness is smaller, while the section moment of inertia at the non cutting position is larger, and the corresponding stiffness is also larger. In order to calculate the overall stiffness of the straight bevel gear blank in the process of gear cutting, the equivalent stiffness of the straight bevel gear blank is calculated by using the method of bending strain energy equivalence.
The bending strain energy equivalent stiffness method is to treat the variable section straight bevel gear blank in gear cutting as an equal section beam with the same blank length, make the two structures have equal bending strain energy in calculation, then calculate the equivalent stiffness of the dissected straight bevel gear blank, and equivalent the complex variable section straight bevel gear blank to a simple equal section beam, Then the equivalent stiffness of variable section straight bevel gear blank in the machining process is solved.
When the straight bevel gear blank is bent and deformed due to the change of internal stress during machining, it is assumed that the bending moment acting on both ends of the straight bevel gear blank is m, and the section angle of the straight bevel gear blank caused by the bending moment is θ, Of which:
The formula for calculating the stored strain energy in the split wheel blank is:
The simultaneous formula can obtain:
However, in practice, the main deformation form of straight bevel gear split wheel blank is bending deformation, and its section angle θ The value of is not equal at different positions of the straight bevel gear blank, and changes along the length direction of the straight bevel gear blank. Therefore, an arbitrarily small unit can be taken along the length direction of the straight bevel gear blank, so that the length of each unit is DX, and the included angle at both ends of this unit is:
After integrating the rotation angle expression at both ends of the unit along the length of the straight bevel gear split wheel blank, the bending strain energy of the whole straight bevel gear split wheel blank can be obtained by substituting into the formula:
The equivalent bending section of U1 and U2 can be divided into the equivalent bending section of U1 and U2, respectively ε = U1-U2, there are:
Where Y1 (x) and Y2 (x) are the deflection curve equations of the straight bevel gear split wheel blank and the equivalent equal section beam respectively, and I1 and I2 are the section moment of inertia of the straight bevel gear split wheel blank and the equivalent equal section beam respectively.
Among them, the deflection curve equation Y2 (x) of equivalent equal cross-section beam is easy to obtain. The deflection curve equation Y2 (x) of the equivalent equal section beam is taken as the first-order approximation of the deflection curve equation Y1 (x) of the straight bevel gear split wheel blank ε= 0 to calculate the equivalent section moment of inertia I2 of the straight bevel gear split wheel blank.