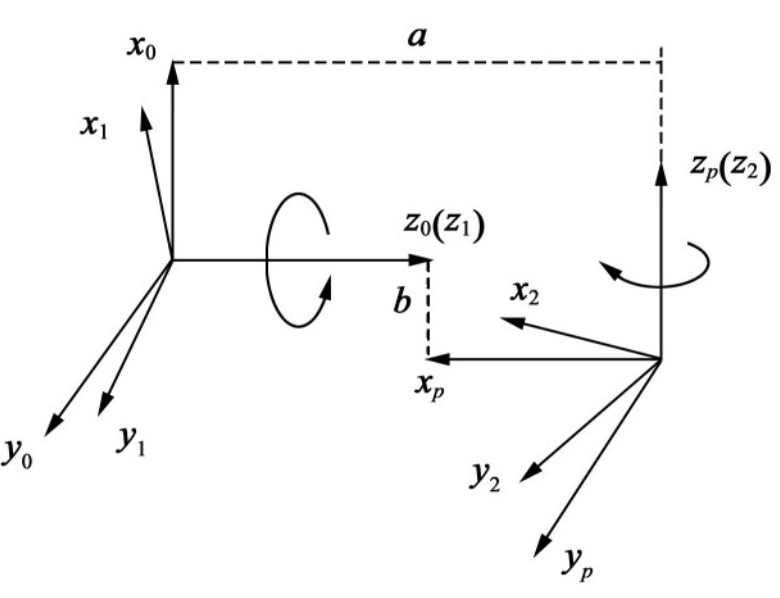
Establish the right-hand coordinate system, as shown in Figure 1. S (o-xyz) and S (oxpypzp) are the main and driven fixture coordinate systems respectively, expressed as s and sp. S (o-x1y1z1) and S (o-x2y2z2) are the coordinate systems which are fixedly connected with the driving wheel and the driven wheel respectively, which are expressed as S1 and S2. At the initial engagement time, S1 and S2 coincide with s and SP respectively. The main and driven wheels rotate around Z-axis and ZP axis with constant angular velocity of ω 1 and ω 2 respectively. After t-step, the rotation angles of the main and driven wheels are respectively ϕ 1 and ϕ 2. The distance between X and ZP is a, and the distance between Z and X is B.
According to the defined coordinate system and parameters, through homogeneous transformation, the transformation matrix from coordinate S1 to coordinate S2 can be obtained as follows:
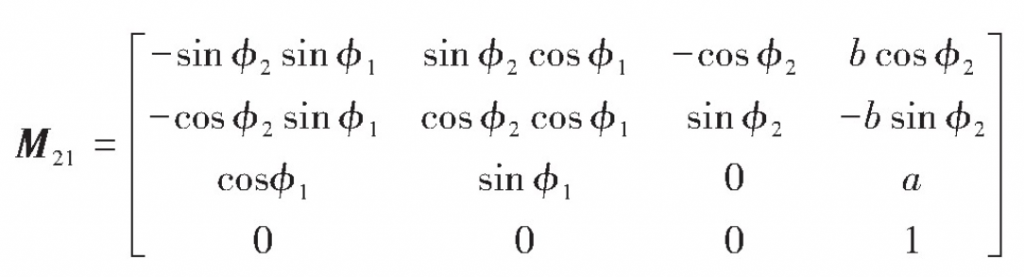
The conic helix is selected as the active contact line. In coordinate system S1, the parameter equation is as follows:
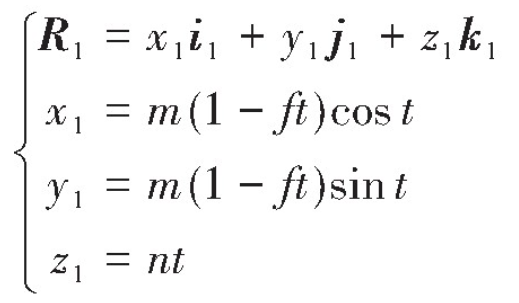
Where, t is the parameter variable, M is the helix radius, n is the pitch coefficient, f is the taper parameter of the conic helix, and I1, J1 and K1 are the base vectors of the coordinate system S1.
According to the meshing theory of space curve, the parameter equation of driven contact line in coordinate system S2 is as follows:
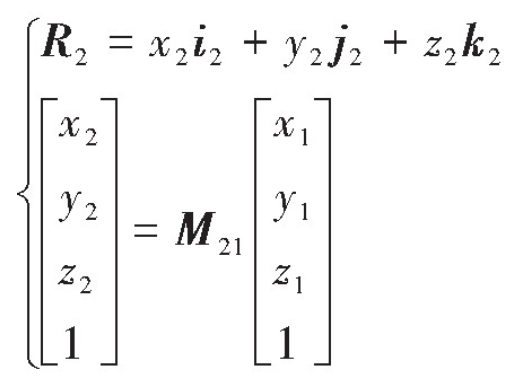
Where M21 is the transformation matrix from coordinate system S1 to coordinate system S2; I2, J2 and K2 are the base vectors of coordinate system S2.
