Only by establishing an accurate mathematical model of gear transmission, can the dynamic simulation analysis of gear transmission process be carried out effectively, and then the system is optimized and designed. According to the model, appropriate methods are adopted to solve it, so as to analyze the vibration performance and dynamic behavior of gear transmission. Considering the time-varying of gear meshing stiffness, transmission error and meshing damping on system vibration and noise, a pair of dynamic models of gear transmission system can be obtained, as shown in Figure.
Let M1 and M2 be the equivalent mass on the meshing line of the gear teeth respectively, KC be the meshing stiffness of the gear teeth, and C be the meshing damping of the gear teeth. PL is the normal load of gear transmission. 1 x and 2 x are the vibration displacement of the gear teeth on the meshing line respectively, X1 and X2 are the vibration speed of the gear teeth on the meshing line respectively, and X1 and X2 are the vibration acceleration of the gear teeth on the meshing line respectively.
According to Newton’s second law and the balance condition of force, the vibration equation of general gear transmission can be obtained as follows:
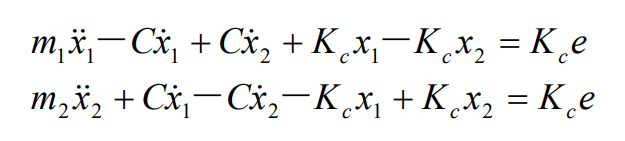
Written in matrix form:
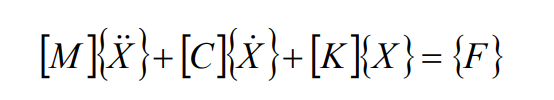
The variation of gear transmission error follows the variation law of simple harmonic motion, so the transmission errors E1 and E2 of gear 1 and gear 2 can be expressed as:
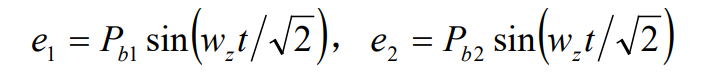
Where PB1 is the base pitch deviation of gear 1; PB2 is the base pitch deviation of gear 2; WZ is the meshing frequency of gear transmission.

