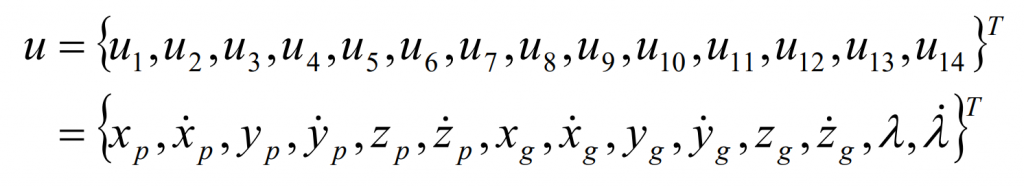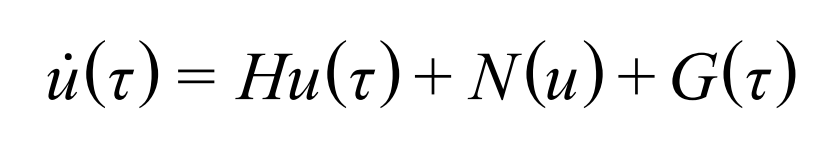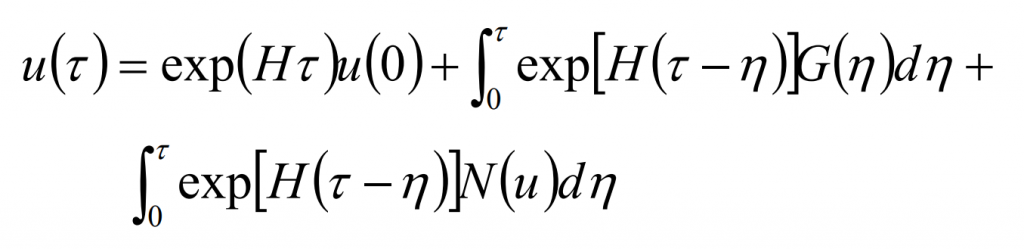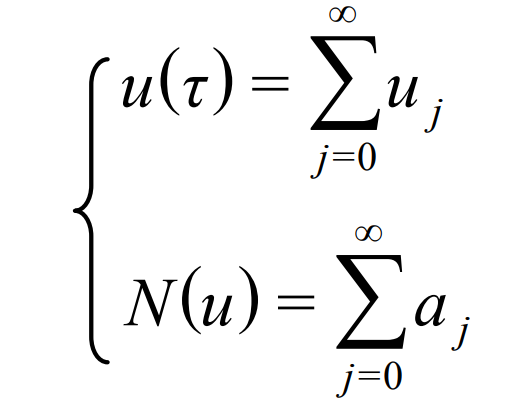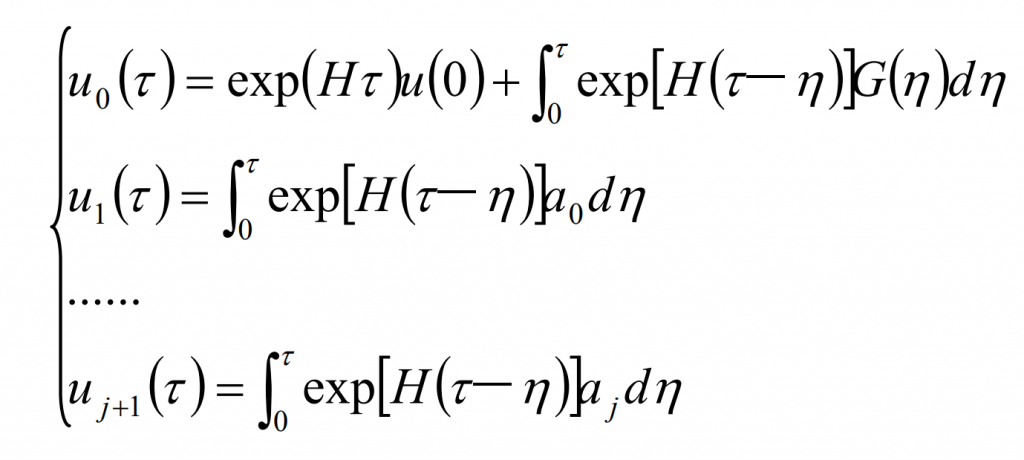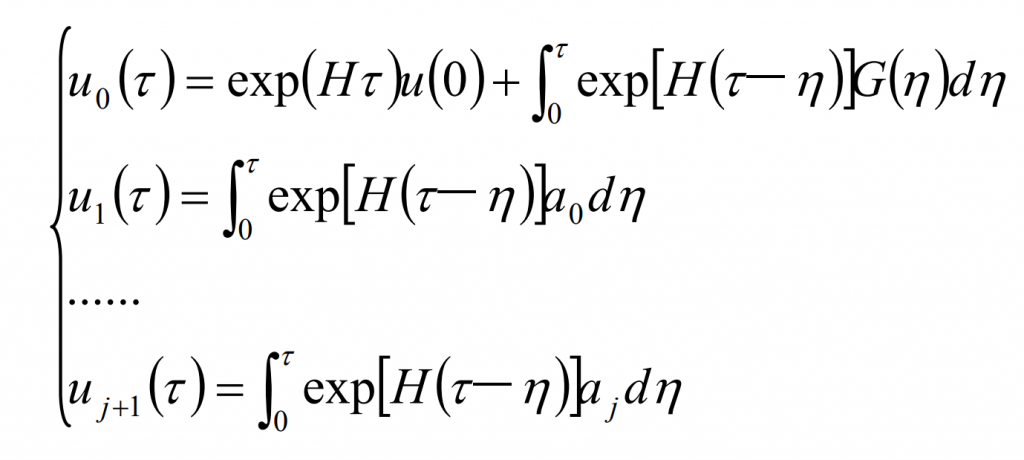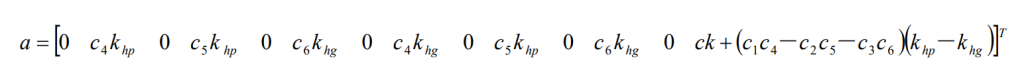For a long time, because there is no effective mathematical method to solve the dynamic equation of straight bevel gear, most modeling methods study the straight bevel gear system as a discrete elastic system, and the established dynamic equations also belong to ordinary differential equations, without considering the nonlinear factors in the process of gear meshing. However, with the development of the nonlinear vibration theory of straight bevel gears, some studies have begun to establish the vibration analysis model of straight bevel gears including a variety of nonlinear factors.
Generally, there are two mathematical methods to solve the nonlinear dynamic equations of straight bevel gear transmission: analytical analysis method and numerical analysis method. Analytical methods include shooting method, piecewise linearization method and so on. Numerical analysis methods are also widely used in the analysis and solution of vibration differential equations of straight bevel gear pairs. Numerical analysis methods mainly include straight bevel gear integration method, direct integration method, Runge Kutta method and so on.
Decompose the differential equation required to be solved into several parts, decompose the nonlinear term in the equation into multiple polynomials, solve each polynomial by using the inverse operator method to obtain several low-order solution components, and then deduce several high-order solution components. By analogy, we can obtain the approximate solution or even accurate solution of the equation, This method for solving nonlinear differential equations is called Adomian decomposition method, which is also a kind of direct integration method. In addition, the inverse operator method is easy to calculate and has good convergence. It is generally used to solve complex nonlinear differential equations [. According to the calculation process and characteristics of this method, the decomposition method is used to solve the dynamic equation of straight bevel gear. The specific solution process is as follows:
Introducing state variables:
Then the formula can be rewritten into the following equation of state:
Where, h is the matrix of linear terms, n (U) is the vector including nonlinear terms, G( τ) Is the vector including the excitation term.
The analytical solution of the formula is:
There are unknown state variables on the left of the above formula. In order to obtain the explicit expression of, let:
Where, AJ is Adomian polynomial.
Substitute the formula and make:
Then the displacement and velocity response of the dynamic equation of straight bevel gear is:
The number of terms n depends on the convergence accuracy, which is generally 5 ~ 6.
According to the established dynamic equation of straight bevel gear, the corresponding Adomian polynomial is obtained as follows:
Where a is a constant vector and its expression is: