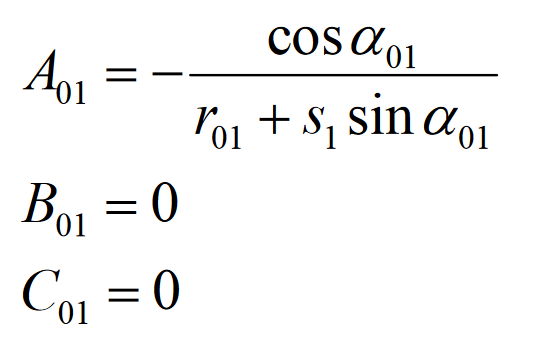The hypoid gear small wheel is machined by the denaturing method. The method of establishing the tooth surface equation of the small wheel is the same as that of the large tooth surface equation, but in addition to the general coordinate system transformation, the function of the deformation mechanism should be considered. The machining coordinate system of hypoid gear pinion is established as shown in the figure.

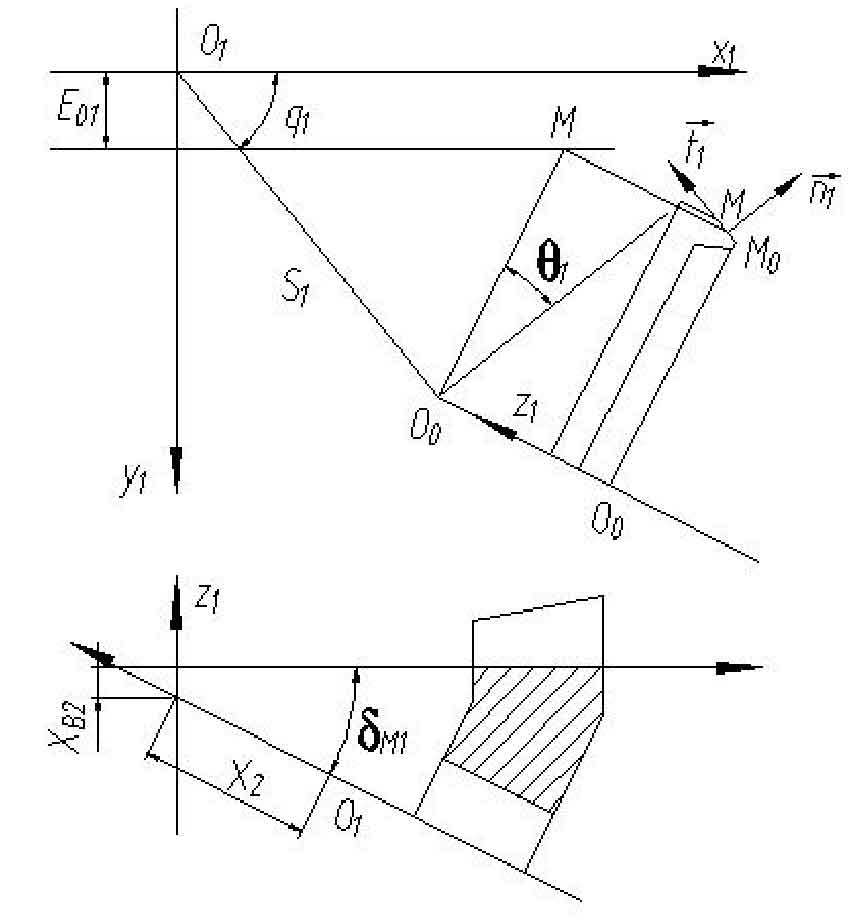
Because the hypoid gear pinion is processed by double-sided method, that is, only one tooth surface of the hypoid gear pinion is processed each time, and the other tooth surface of the hypoid gear pinion is processed after readjusting the processing parameters. Therefore, two sets of processing parameters are required for processing the hypoid gear pinion. This is precisely why in the TCA analysis, if the analysis result is not ideal, only the processing parameters of the hypoid gear pinion need to be adjusted, This can reduce the workload. Taking the concave surface of the hypoid gear pinion as an example, the rocker angle when machining the hypoid gear pinion is q1, θ 1 is the phase angle of the tool tip. The tool tip radius for machining hypoid gear pinion is O0M0=r01, and the vector formula of O0M0 in the machine coordinate system O1x1y1z1 is:

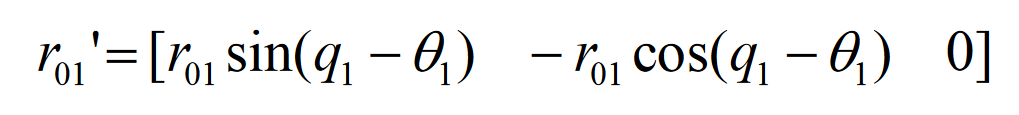
The normal vector and generatrix direction unit vector of point m on the generatrix of hypoid gear cutting cone are:

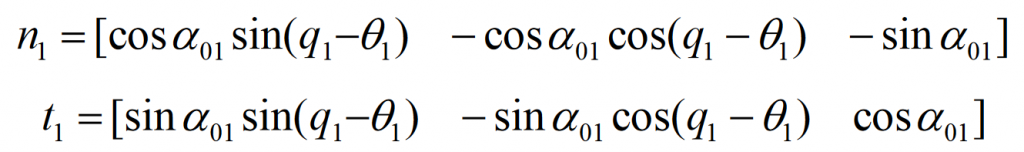
If the distance from a point on the cutting cone to the tool tip is S1, the equation of any point m on the cutting cone is:

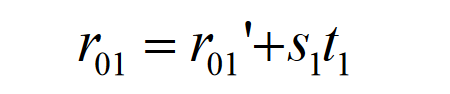
At point m, the normal curvature and short-range torsion along T1 x N1 and T1 are: