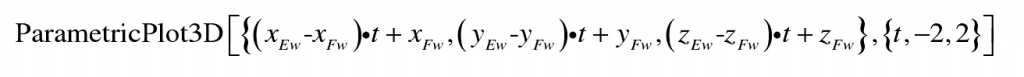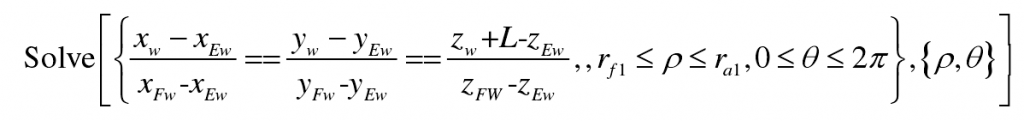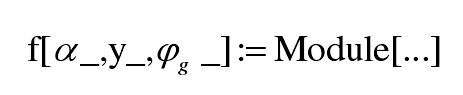By transforming the matrix MWG, the points e (Xe, ye, Ze) and f (XF, YF, ZF) in the gear coordinate system SG are transformed into the gear hob coordinate system WS. According to the normal equation and formula of the gear tooth surface, the normal of any point on the gear tooth surface can be drawn by using the command of parametricplot3d drawing three-dimensional parameter diagram in Mathematica Software:
When a certain point on the gear tooth surface is determined( α, y, φ g) Can be obtained by parameters( ρ,θ) Represents the intersection coordinates of the normal of the gear tooth surface and the involute helical surface of the gear hob. Simultaneous formula. Solve the intersection of the normal of the gear tooth surface and the involute helical surface of the gear hob through the solve equation command:
Where l is the gear angle φ G the translation distance of the corresponding gear hob along the axis.
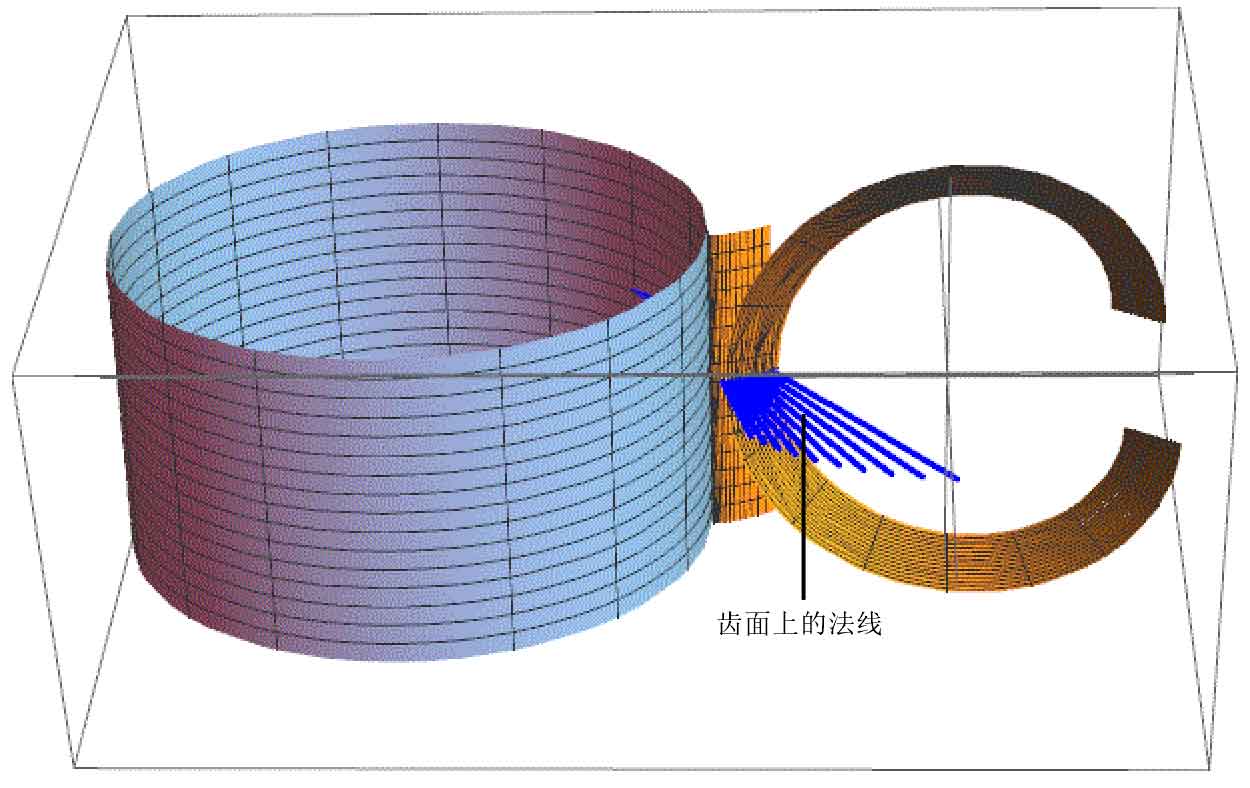
In the gear hob coordinate system: SW (ow: XW, YW, ZW), the rotation angle of the gear φ When g = 0, the intersection of the normal on the tooth profile with y = 0 and the involute helical surface of the gear hob is solved, as shown in the figure.
Based on Mathematica software, the unfolding length of any point on the tooth profile is obtained through module […] module function. The function has three independent variables. The first independent variable is the pressure angle on the gear tooth surface α , The second independent variable is y, the first two independent variables determine a certain point on the tooth surface, and the last independent variable is the rotation angle of the gear φ g 。 The gear angle is φ g. On the gear tooth surface( α, y) The expansion length of the point is calculated as follows:
The module […] function contains the normal equation of a point on the gear tooth surface, the rotation angle relationship between the gear hob and the gear according to the fixed transmission ratio, the solution equation of the intersection between the normal of the gear tooth surface and the involute helical surface of the gear hob, and the distance from the point on the tooth profile to the intersection with the involute helical surface of the gear hob along its normal direction, that is, the unfolded length of the point.