In order to explain the influence of different deviation values on the contact line error and tooth profile of cylindrical gear under different types of relative position deviation between grinding wheel and cylindrical gear workpiece, the following examples are analyzed. The left spiral tooth surface of the right-hand cylindrical gear is selected as the analysis object.
In the example calculation, according to the formula, the theoretical contact line equation and the theoretical tooth surface equation can be obtained respectively. According to the formula, the actual contact line equation and the actual tooth surface equation of grinding wheel and cylindrical gear can be obtained under the condition of different types of relative position deviation.
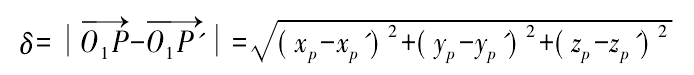
By drawing both theoretical and actual tooth profile models in Mathematica software, the size of contact line error of cylindrical gear can be calculated, and the law of tooth profile error of cylindrical gear can be analyzed.
1) Analysis of tooth profile error caused by Δ SX. When the offset Δ SX of grinding wheel center along x2 axis is -0.20, 0.20 mm, the error Tooth profile is shown in Fig. 1. According to the formula, the tooth profile errors at the corresponding meshing points on the contact line are all 0.200 mm. When Δ SX < 0, the helix radius of contact wire increases; when Δ SX > 0, the helix radius of contact wire decreases. As can be seen from figure 8, the existence of Δ SX will cause tooth thickness error. When Δ SX < 0, the addendum tooth thickness increases and the root tooth thickness decreases; when Δ SX > 0, the addendum tooth thickness decreases and the root tooth thickness increases. At the same time, the size of tooth profile error will not change along the direction of tooth width.
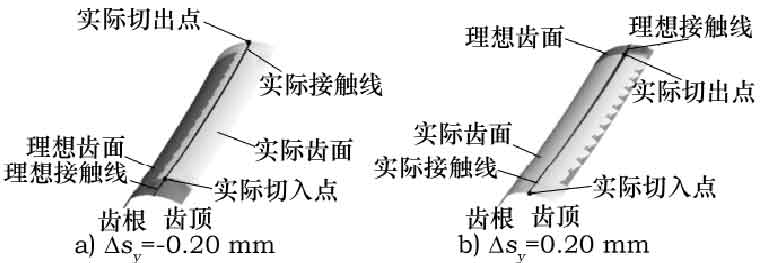
2) Analysis of tooth profile error caused by Δ sy. When the offset of grinding wheel center along Y2 axis Δ sy = – 0.20, 0.20 mm, the error Tooth profile is shown in Figure 2. According to the formula, the tooth profile errors at the corresponding meshing points on the contact line are all 0.190 mm, and Δ sy has little effect on the helix radius of the contact line, but it will change the positions of the entry and exit points of the grinding wheel. It can be seen from Figure 2 that the influence of Δ sy on the tooth thickness is far less than that of Δ SX. When Δ sy < 0, the actual entry point of the grinding wheel will be behind the theoretical entry point; when Δ sy > 0, the actual entry point of the grinding wheel will be ahead of the theoretical entry point.
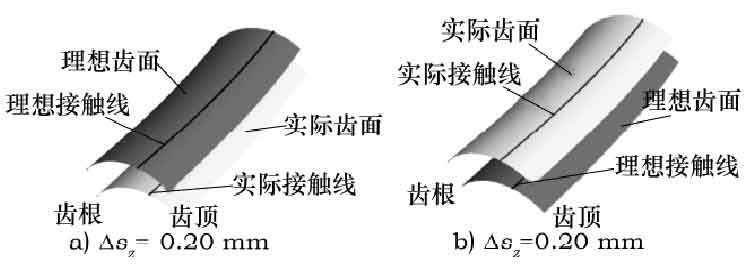
3) Analysis of tooth profile error caused by Δ Sz. When the offset of grinding wheel center along Z2 axis Δ SZ = – 0.20, 0.20 mm, the error Tooth profile is shown in Figure 3. According to the formula, the tooth profile errors at the corresponding meshing points on the contact line are all 0.200 mm. It can be seen from Figure 3 that the existence of Δ SZ will cause tooth thickness error. When Δ SZ < 0, the tooth thickness decreases; when Δ SZ > 0, the tooth thickness increases. At the same time, the size of tooth profile error will not change along the direction of tooth width.
4) Analysis of tooth profile error caused by Δ α. When the inclination error Δ α produced by the grinding wheel axis rotating around the X2 axis is – 0.01 ° and 0.01 ° respectively, the error Tooth profile is shown in Fig. 4. According to the formula, the tooth profile errors at the corresponding meshing points on the contact line are all 0.012 mm. As can be seen from Figure 4, Δ α will cause tooth thickness error. When Δ α < 0, the tooth thickness decreases; when Δ α > 0, the tooth thickness increases. At the same time, the size of tooth profile error will not change along the direction of tooth width.
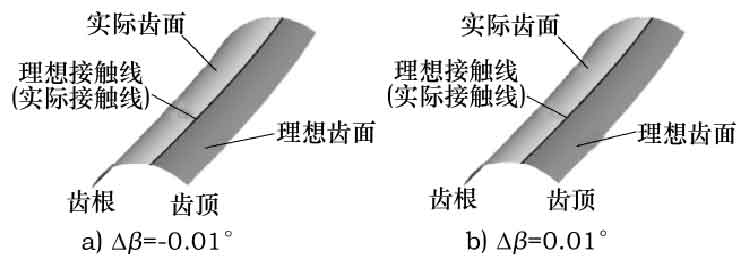
5) Analysis of tooth profile error caused by Δ β. When the inclination error Δ β caused by the grinding wheel axis rotating around Y2 axis is – 0.01 ° and 0.01 ° respectively, the error Tooth profile is shown in Fig. 5. According to the formula, the tooth profile error values at the corresponding meshing points on the contact line are all 0, and Δ β will not cause the contact line error. It can be seen from Fig. 5 that no matter Δ β < 0 or Δ β > 0, the tooth thickness of tooth tip will decrease and that of tooth root will increase; meanwhile, the influence of Δ β on tooth thickness is far less than that of Δ α.