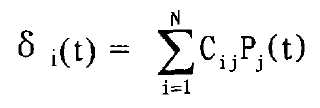The flexibility matrix method is used to solve the three-dimensional elastic contact problem. The solution of the contact problem of the contact body can be completed by calling the finite element once to obtain the flexibility value of the unit force acting on the possible contact points of each contact body.

The stiffness matrix can be obtained by finite element method. Since the stiffness matrix is divided into 400 elements, 840 nodes, 2520 rows and columns. In the case of small error in the calculation results, it is not necessary to inverse the huge stiffness matrix to obtain the flexibility matrix, but only divide the mesh on the tooth surface, take the number of all nodes m in the tooth surface mesh, make the unit normal load act on each tooth surface node in turn, calculate the deformation of each node, and obtain a tooth surface flexibility matrix of m x m order:

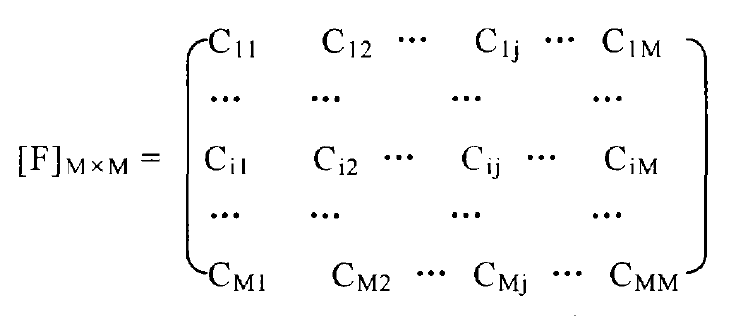
Where CIJ is the deformation (flexibility) at point I when the unit load is applied at point J. There are 273 gear tooth surface nodes studied, and the flexibility matrix M = 273. The flexibility matrix of tooth surface nodes is obtained by using the formula. For example, the load PJ (T) acts on point J, and the deformation at point I is:

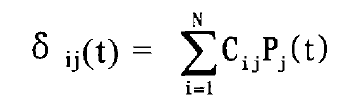
When there are n points on the tooth surface, there is a load PJ (T), j = 1,2,3… N. For example, when n tooth surface nodes of the gear pair participate in meshing, the deformation at point I is: