The design methods of non-circular gear tooth profile mainly include envelope method, hobbing tooth profile normal method and shaping tooth profile normal method. The envelope method is to solve the tooth profile by curve fitting the hobbing boundary of the cutter, which has a large amount of calculation and complex algorithm design; The normal method of gear shaper profile is similar to the normal method of gear hobbing profile, and the numerical algorithm is relatively simple. The normal method of gear shaper profile is also suitable for the design of concave and convex non-circular gears, so the normal method of gear shaper profile is adopted in this paper. When designing the module and number of teeth of non-circular gear, undercutting should be avoided as far as possible. Firstly, the pitch curve curvature radius of non-circular gear is calculated. If we use the analytic method to solve the problem, we need to calculate the second derivative of the nodal curve, so the calculation is complex.
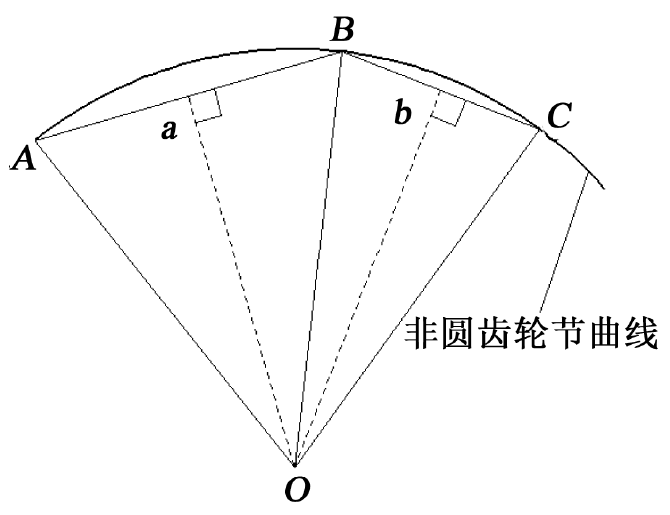
As shown in Figure 1, three adjacent points a, B and C are randomly selected on the pitch curve, and the coordinates are (Xi, Yi), (Xi + 1, Yi + 1) and (Xi + 2, Yi + 2). Points a and B are the midpoint of AB and BC respectively. If OA ⊥ AB and ob ⊥ BC are known, then when a, B and C are close enough, the length of OA is close to the curvature radius of pitch curve ABC; Let the o coordinate of the point be (x, y), the slope of OA be K1, the slope of OB be K2, and the radius of curvature of the nodal curve ABC be ρ , The results are as follows:
The curvature radius of the pitch curve can be obtained by substituting the coordinates of the pitch curve calculated by the formula into the formula. The calculation results are shown in Fig. 2-3, where ρ 1、 ρ 2 is the pitch curve curvature radius of the driving and driven noncircular gears. ρ 1 min ρ 1 min=46.459mm , ρ 2 min ρ 2 min=22.367mm .
According to the description, involute gear machining does not occur undercutting should meet the formula. Take the pressure angle of gear shaper cutter here α n=20 ° 、 The coefficient of addendum height h * a = 1 and the coefficient of addendum clearance C * 0.25. Respectively ρ 1 min and ρ The module Mn1 of driving non-circular gear is less than 4.348, and the module Mn2 of driven non-circular gear is less than 2.093. The minimum number of teeth without undercutting is calculated according to the formula, substituting S1, S2, mn1max and mn2max, the minimum number of teeth of driving non-circular gear is 36.628, and the minimum number of teeth of driven non-circular gear is 76.088. In order to prevent undercutting of two noncircular gears, the number of teeth Z of both gears is taken as 77; Substituting Z value into the formula, the module Mn of gear shaper cutter is 2.068. When the number of teeth ZC = 20, the pitch circle diameter DC = mnzc = 41.364mm, the base circle diameter DCB = DCCOs α n=38.869mm .