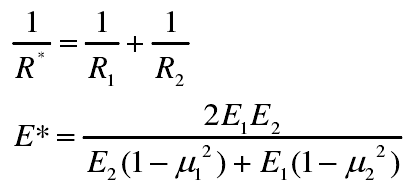Under the condition of non lubrication, according to Hertz theory, the contact geometry of gear tooth surface can be transformed into a pair of equivalent contact cylinders. The radius R1 and R2 of the two cylinders are respectively equal to the curvature radius of the two tooth profiles at the node, and the model radius R * of the equivalent contact is obtained from the radius of the two cylinders. The distribution of Hertz contact pressure P (x) and tangential contact load Q (x) are as follows:
Where: the x-axis direction is horizontal with the contact area of the gear pair, and 0 point is in the center of the contact area; FN is the normal force per unit width; B is the contact half length; P0 is the maximum normal contact load; E * and R * are the equivalent Young’s modulus and radius of contact, respectively
Where: E1, E2 μ 1、 μ 2 is the young’s modulus and Poisson’s ratio of the two gears in contact. Because the material properties of the two gears used in this paper are the same, E1 = E2 = E, μ 1= μ 2= μ。 In the lubrication contact process, the contact pressure between gear pairs will be different, as shown in Figure 1, mainly reflected in the inlet area, outlet area and secondary pressure peak. At the same time, under the condition of elastohydrodynamic lubrication, the gear pair is separated by a layer of oil film, which will transfer the contact pressure. Therefore, considering the condition of EHL, the normal load between gears is EHL pressure, and the tangential load is the product of EHL pressure and friction coefficient F.