In order to study the influence of time-varying meshing stiffness and sliding friction force on the dynamic response of gear system, a simplified dynamic model of gear transmission system in Fig. 2-1 is established by using lumped parameter method. The model is a nonlinear gear dynamic model with six degrees of freedom considering the influence of sliding friction force. For the simplification of the gear model, the following conditions are assumed to be true:
1) The driving gear and driven gear are assumed to be rigid disks;
2) The shaft bearing stiffness along and perpendicular to the gear line of engagement is assumed to be a lumped mass element and connected to a rigid housing;
3) The Coulomb friction model is assumed to have a constant friction coefficient μ.
Considering the time-varying meshing stiffness and sliding friction force of the gear surface, the dynamic model of the gear system with six degrees of freedom is established as shown in the figure. The definition of the relevant parameters of the dynamic model of the gear system is as follows.
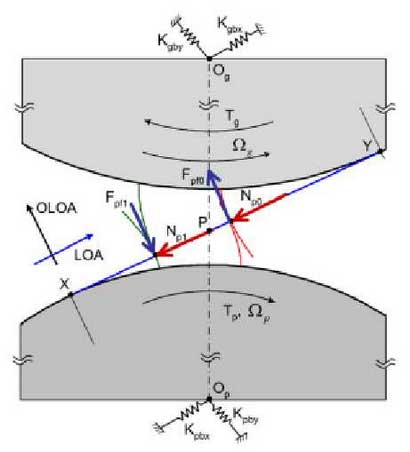
The six degrees of freedom are the rotation of the driving and driven gears (θ P and θ g), the translation of the driving and driven gears along the meshing line (χ P and χ g), and the translation of the driving and driven gears perpendicular to the meshing line (YP and YG). Among them, the x-axis direction is parallel to the gear meshing line, TP / TG is the driving / braking torque, Ω P / Ω G is the working speed of the driving / driven gear, JP / JG is the moment of inertia of the driving gear / driven gear, MP / Mg is the mass of the driving gear / driven gear, KPX, KPY, kgx, kGy are the bearing support stiffness of the main and driven gears respectively, CPX, CPY, kgx and kGy Is the corresponding bearing damping, Ki is the meshing stiffness of the ith pair of gears, CI is the damping of the ith pair of gears.
