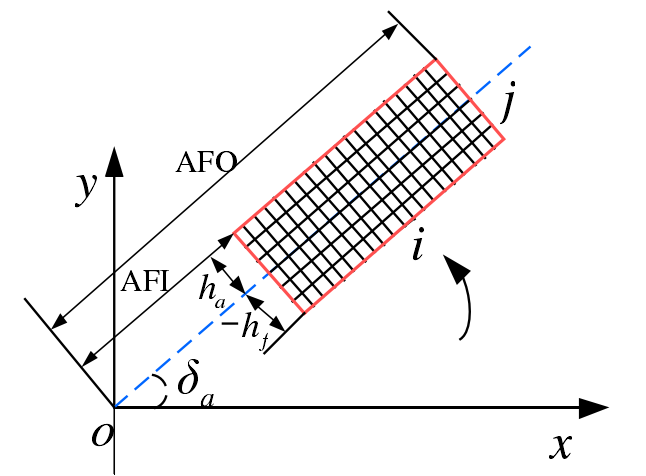
As the tooth surface of FH hypoid gear is relatively complex, it is difficult to mesh directly on the tooth surface, which requires mesh generation on the rotating projection surface. The rotating projection surface of the gear is shown in Fig. 3-4. The origin in the figure is the vertex of the bevel angle of the gear, δ a represents the bevel angle, ha represents the top height of the tooth, HF represents the root height, AFI represents the inner cone distance, and AFO represents the outer cone distance. If n meshes are divided in the direction of tooth height and M grids in the direction of tooth direction, then each mesh point on the tooth surface can be expressed as follows:
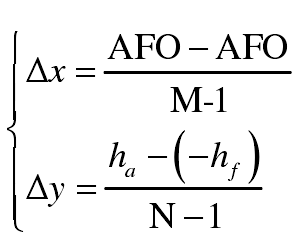
In Cartesian coordinate system, the coordinate values of mesh points on tooth surface can be expressed as follows:
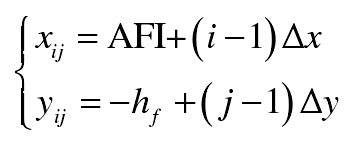
According to the coning angle δ a, the coordinates of the mesh points on the tooth surface are rotated to the rotation projection surface, and the coordinate values on the rotation projection surface can be expressed as follows:
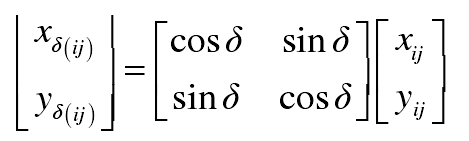
The relationship between the coordinate values of the mesh points on the tooth surface and the coordinate values on the rotating projection surface are as follows:
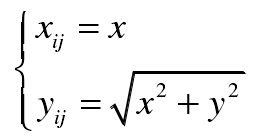
Where x, y and Z are the coordinate values of mesh points on the tooth surface.