1. Effect of torque on coincidence degree
Calculate the large wheel torque as 1000 n respectively · m、2 000 N · m、3 000 N · m、4 500 N · m、6 000 N · M and 9 000 n · M time-varying equivalent meshing parameters under forward driving condition. With the increase of torque, the deformation and coincidence degree of hypoid gear increase, as shown in Figure 1.
2. Effect of torque on the position of equivalent meshing point
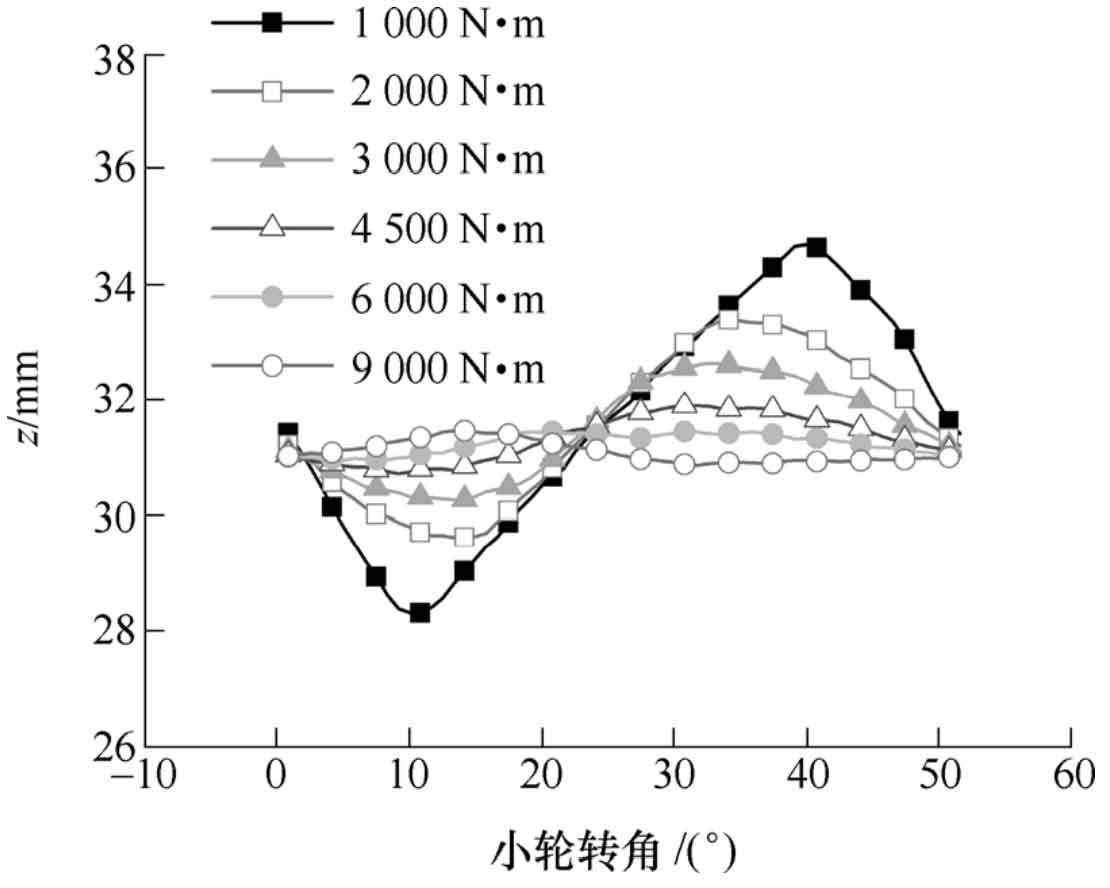
The coordinate change curve of the spatial position of the equivalent meshing point corresponding to each torque is shown in Fig. 2 ~ 4. With the increase of torque, the coincidence degree increases, the change range of the position of the equivalent meshing point decreases, and the meshing state of hypoid gear is more stable. As the same as the above analysis, since the distance of the meshing area moving along the long direction of the gear tooth is greater than the tooth height direction, the change of X coordinate under each torque is greater than that in the other two directions.
3. Effect of torque on equivalent meshing force
The variation curves of each component of the action direction vector of the equivalent meshing force corresponding to each torque are shown in Fig. 4 ~ 6. With the increase of torque and coincidence degree, the variation amplitude of the acting direction vector of equivalent meshing force also decreases, and the meshing state of hypoid gear is more stable.
4. Influence of torque on transmission error
The linear displacement of the equivalent meshing point along the action direction of the meshing force and the variation relationship of the transmission error with the load are shown in Fig. 7. With the increase of torque, the meshing force of the hypoid gear increases, resulting in the increase of the deformation of the hypoid gear and the increase of the transmission error.
5. Effect of torque on equivalent meshing stiffness
The variation curve of time-varying secant meshing stiffness corresponding to different torques obtained by the traditional method is shown in FIG. 8. The time-varying equivalent tangent meshing stiffness curve under each torque obtained by the finite element method in this paper is shown in FIG. 9. With the increase of torque, the coincidence degree increases and the deformation of hypoid gear increases, resulting in the increase of secant meshing stiffness and tangent meshing stiffness, Comparing the average secant meshing stiffness and the average tangent meshing stiffness under different torques, as shown in Figure 10, the tangent stiffness is significantly greater than the secant stiffness, and the meshing stiffness of hypoid gear obtained by traditional method is too small, which is inaccurate. In addition, the average meshing stiffness decreases with the increase of torque, which is determined by the nonlinear characteristics of meshing stiffness of hypoid gear.
It can also be seen from Figure 9 that the load torque of the large wheel is 1000 n · m、2 000 N · M and 3 000 n · The variation range of tangent stiffness at M is significantly greater than 4500 n · m、6 000 N · M and 9 000 n · According to the coincidence curve in Figure 1, when the load torque of large wheel is 1000 n · m、2 000 N · M and 3 000 n · M, the coincidence degree is less than 2, and the hypoid gear is in the alternating meshing state of 1 to 2 pairs of teeth, when the torque is 4500 n · m、6 000 N · M and 9 000 n · M, the coincidence degree is greater than 2, and the hypoid gear is in the state of alternating meshing of 2 to 3 pairs of teeth. Although the stiffness increases, the variation range of stiffness in one cycle decreases, which has an important impact on the dynamic characteristics of the hypoid gear system.
6. Conclusion
(1) The finite element model of hypoid gear is analyzed by using the general finite element analysis software ABAQUS. The correctness of the modeling and analysis is verified by comparing with the classical TCA analysis method and the loading meshing imprinting test.
(2) Based on the LTCA analysis results, the time-varying equivalent meshing point position, the size and direction of time-varying equivalent meshing force, the linear displacement transmission error along the action direction of equivalent meshing force and the equivalent meshing stiffness curve of hypoid gear under torque load are calculated, which provides a basis for the dynamic modeling and analysis of hypoid gear system.
(3) Using the central difference method to obtain the tangent stiffness of hypoid gear can more accurately reflect the gear meshing stiffness characteristics, and then truly reflect the dynamic characteristics of hypoid gear system.
(4) The influence of system torque on meshing parameters is studied. With the increase of torque, the coincidence degree of hypoid gear increases, the changes of equivalent meshing position and direction vector of equivalent meshing force decrease, and the meshing state is more stable. While the meshing force of hypoid gear increases, the deformation of hypoid gear increases, and the transmission error increases, The meshing stiffness of hypoid gears also increases. The research shows that the change of tangent meshing stiffness in a cycle when the coincidence degree is greater than 2 is significantly less than that when the coincidence degree is less than 2.