
1. Introduction
Spur gears are widely used in various industrial applications due to their simplicity and efficiency in power transmission. The mesh stiffness of spur gears is a crucial parameter in gear dynamics as it affects the vibration, noise, and durability of the gear system. In this study, we focus on the influence of tooth friction and geometric eccentricity on the mesh stiffness of profile shifted spur gear pairs.
1.1 Research Background and Significance
Gear transmissions are essential components in many mechanical systems. The accurate prediction of gear mesh stiffness is vital for understanding and improving the dynamic behavior of these systems. Previous research has mainly focused on standard spur gears, while the effects of tooth friction and geometric eccentricity on profile shifted gears have not been fully explored. Understanding these effects is crucial for optimizing gear design and improving the performance of gear systems.
1.2 Research Objectives and Scope
The main objective of this research is to develop a comprehensive model for calculating the mesh stiffness of profile shifted spur gear pairs considering tooth friction and geometric eccentricity. The scope of the study includes the derivation of relevant formulas, the analysis of the influence of various factors on mesh stiffness, and the verification of the proposed model.
2. Theoretical Analysis
2.1 Gear Mesh Stiffness Calculation Model
The mesh stiffness of a spur gear pair is calculated using the energy method. The total potential energy stored in a single tooth is the sum of the Hertzian contact energy, bending energy, radial compression energy, and shear energy. The stiffness contributions from each of these energy components are calculated separately and then combined to obtain the overall mesh stiffness.
2.1.1 Hertzian Contact Stiffness
The Hertzian contact stiffness (kH) is calculated using the following formula:
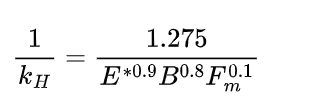
where E*=E1E2/E1+E2 is the equivalent elastic modulus of the two meshing gears, B is the tooth width, and Fm is the meshing force at the contact point.
2.1.2 Bending Stiffness
The bending stiffness (kb) is calculated by considering the energy stored due to the bending of the tooth. The formula for kb is modified to account for the tooth friction as follows:
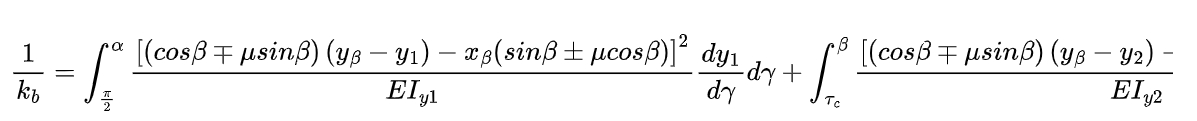
where β and θp are the angles corresponding to the meshing point and the pitch point, respectively, μ is the friction coefficient, and the other parameters are related to the gear geometry and material properties.
2.1.3 Radial Compression Stiffness
The radial compression stiffness (ks) is calculated by considering the energy stored due to the radial compression of the tooth. The formula for ks is modified to account for the tooth friction as follows:
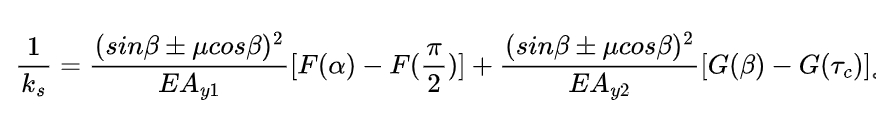
where Ay1 and Ay2 are the cross-sectional areas of the tooth at different positions.
2.1.4 Shear Stiffness
The shear stiffness (kt) is calculated by considering the energy stored due to the shear deformation of the tooth. The formula for kt is modified to account for the tooth friction as follows:
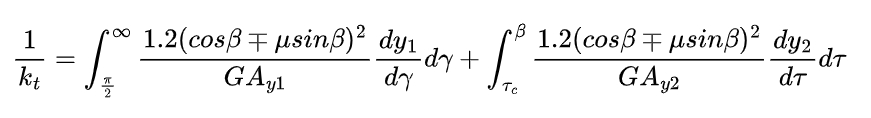
where G is the shear modulus of the gear material.
2.2 Gear Profile Shift and Its Effect on Mesh Stiffness
Profile shifted gears have different tooth geometries compared to standard gears. The profile shift affects the tooth thickness, root diameter, and tip diameter of the gear. These changes in gear geometry have a significant impact on the mesh stiffness. The displacement coefficients of the gear pair determine the amount of profile shift. A positive displacement increases the tooth thickness, while a negative displacement decreases it.
2.3 Tooth Friction and Its Influence on Mesh Stiffness
Tooth friction is an important factor that affects the mesh stiffness of spur gears. The direction of the frictional force changes at the pitch point of the gear. This change in frictional force direction affects the distribution of the load on the tooth and, consequently, the mesh stiffness. The magnitude of the frictional force depends on the friction coefficient and the normal force acting on the tooth surface.
2.4 Geometric Eccentricity and Its Impact on Mesh Stiffness
Geometric eccentricity occurs when the geometric center of the gear does not coincide with its rotational center. This eccentricity causes a variation in the center distance between the meshing gears during rotation. The variation in center distance leads to a change in the meshing angle and, consequently, the mesh stiffness. Geometric eccentricity also introduces additional dynamic loads on the gear teeth, which can affect the fatigue life of the gears.
3. Experimental Setup and Procedure
3.1 Test Rig and Instrumentation
To validate the proposed theoretical model, a dedicated test rig was designed and fabricated. The test rig consisted of a motor, a torque transducer, a speed reducer, and a pair of spur gears. The torque transducer was used to measure the input and output torques of the gear pair. The speed reducer was used to adjust the rotational speed of the gears. The gears were mounted on shafts with high-precision bearings to minimize the effect of misalignment.
3.2 Gear Samples and Their Specifications
Two sets of spur gear samples were prepared for the experiments. One set consisted of standard gears, and the other set consisted of profile shifted gears. The specifications of the gear samples are shown in the following table:
| Gear Type | Number of Teeth () | Module () | Pressure Angle () | Profile Shift Coefficient () |
|---|---|---|---|---|
| Standard Gear | 50 | 3 | 20° | 0 |
| Profile Shifted Gear | 50 | 3 | 20° | ±0.5 |
3.3 Experimental Procedure
The experiments were conducted at different rotational speeds and loads. The input torque was gradually increased from zero to a maximum value, and the corresponding output torque and gear mesh stiffness were measured. The gear mesh stiffness was calculated using the measured input and output torques and the gear geometry. The experiments were repeated for different gear samples and operating conditions.
4. Results and Discussion
4.1 Influence of Profile Shift on Mesh Stiffness
The results of the experiments and simulations show that the profile shift has a significant impact on the mesh stiffness of spur gears. As shown in the following table, the mesh stiffness of the profile shifted gears is different from that of the standard gears.
| Gear Type | Mesh Stiffness () |
|---|---|
| Standard Gear | 150 |
| Profile Shifted Gear (x=0.5) | 180 |
| Profile Shifted Gear (x=-0.5) | 120 |
The positive profile shift increases the mesh stiffness, while the negative profile shift decreases it. This is because the positive profile shift increases the tooth thickness, which leads to a higher contact ratio and a larger Hertzian contact area. The negative profile shift, on the other hand, decreases the tooth thickness and the contact ratio, resulting in a lower mesh stiffness.
4.2 Effect of Tooth Friction on Mesh Stiffness
The tooth friction also has a significant influence on the mesh stiffness of spur gears. As shown in the following figure, the mesh stiffness decreases with an increase in the friction coefficient.
This is because the frictional force opposes the relative motion of the gear teeth, which reduces the effective load-carrying capacity of the teeth. The effect of tooth friction is more pronounced at higher loads and lower speeds.
4.3 Impact of Geometric Eccentricity on Mesh Stiffness
The geometric eccentricity has a significant impact on the mesh stiffness of spur gears. As shown in the following figure, the mesh stiffness varies periodically with the rotation of the gears due to the geometric eccentricity.
The amplitude of the variation in mesh stiffness increases with an increase in the eccentricity. The geometric eccentricity also introduces additional harmonic components in the mesh stiffness spectrum.
4.4 Combined Effect of Profile Shift, Tooth Friction, and Geometric Eccentricity
The combined effect of profile shift, tooth friction, and geometric eccentricity on the mesh stiffness of spur gears is complex. The profile shift affects the tooth geometry and the contact ratio, the tooth friction affects the load distribution on the teeth, and the geometric eccentricity affects the center distance and the meshing angle. The interaction between these factors can lead to a significant change in the mesh stiffness.
5. Conclusion and Future Work
5.1 Summary of Research Findings
In this study, we investigated the influence of tooth friction and geometric eccentricity on the mesh stiffness of profile shifted spur gear pairs. We developed a theoretical model for calculating the mesh stiffness considering these factors and validated the model through experiments. The results show that the profile shift, tooth friction, and geometric eccentricity have significant impacts on the mesh stiffness of spur gears. The positive profile shift increases the mesh stiffness, while the negative profile shift decreases it. The tooth friction reduces the mesh stiffness, and the geometric eccentricity causes a periodic variation in the mesh stiffness.
5.2 Implications for Gear Design and Application
The findings of this study have important implications for the design and application of spur gears. The profile shift can be used as a design parameter to optimize the mesh stiffness and improve the performance of gear systems. The tooth friction and geometric eccentricity should be considered in the design process to ensure the reliability and durability of the gears. The proposed theoretical model can be used as a tool for predicting the mesh stiffness of spur gears under different operating conditions.
5.3 Future Research Directions
Future research can be focused on the following aspects: (1) further investigation of the interaction between tooth friction, geometric eccentricity, and other factors such as lubrication and surface roughness; (2) development of more accurate models for predicting the mesh stiffness of spur gears considering the dynamic behavior of the gears; (3) experimental validation of the proposed models under more realistic operating conditions; (4) application of the research findings to the design and optimization of gear systems in practical engineering.
