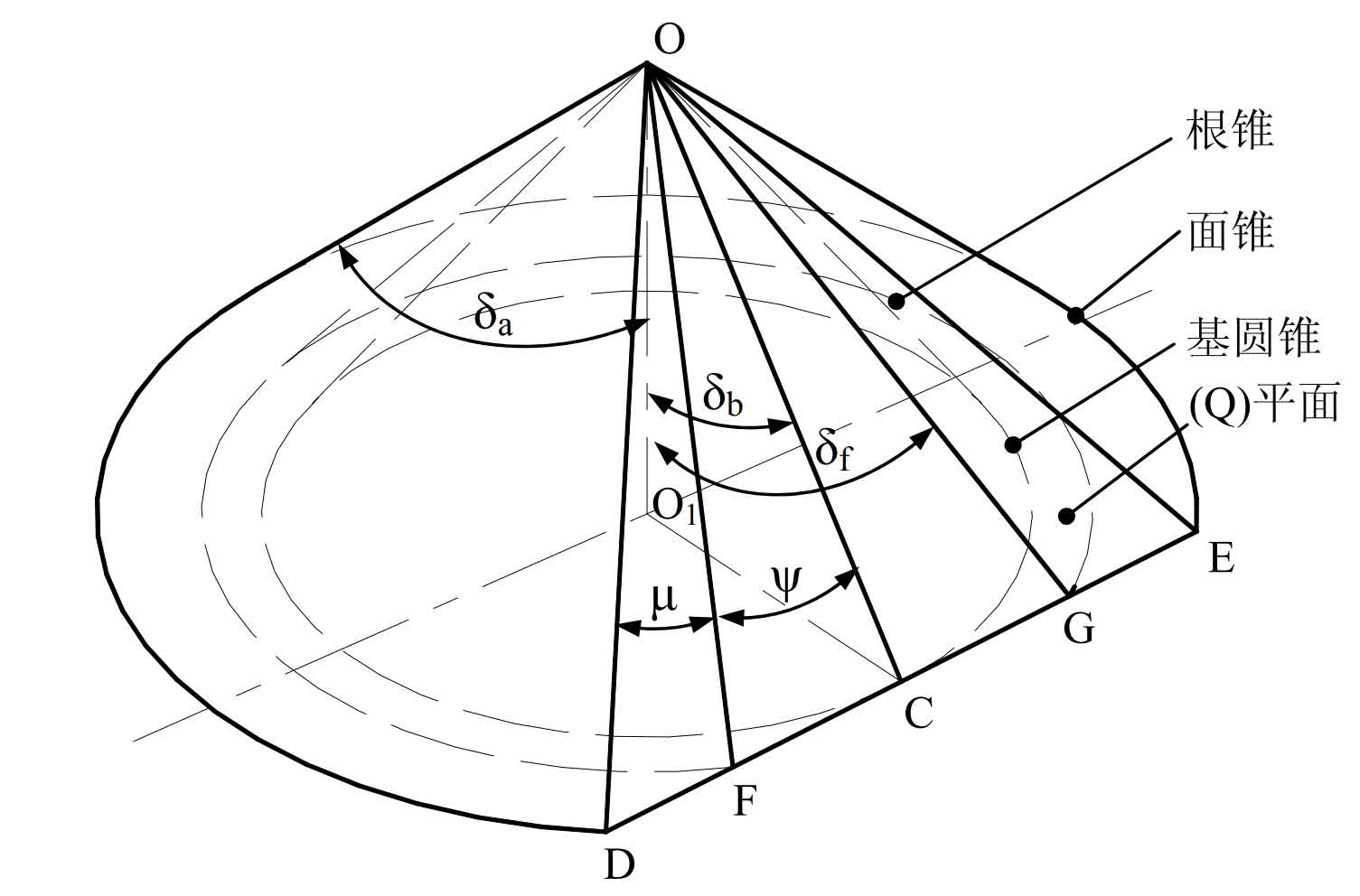
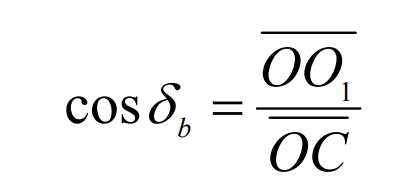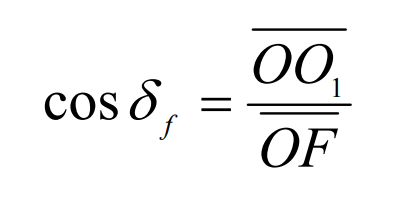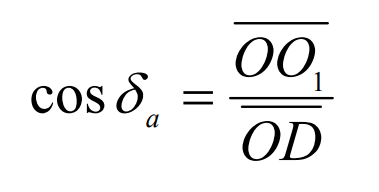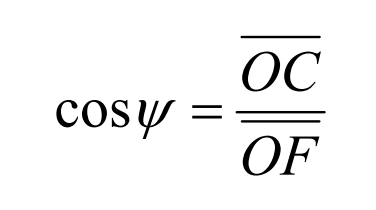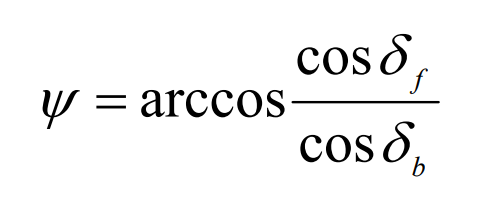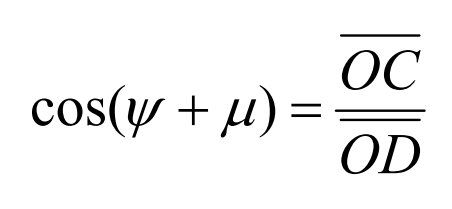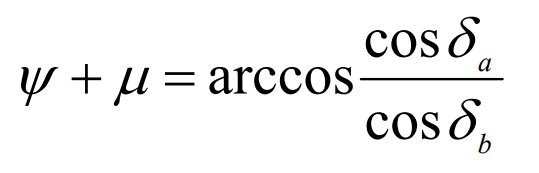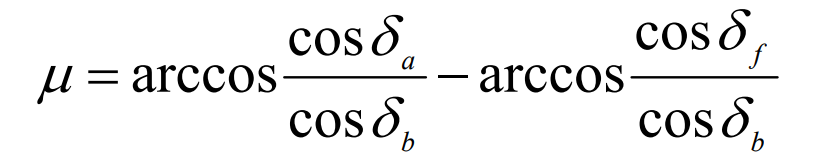For spiral bevel gears with contracted teeth whose base cone, root cone, pitch cone and face cone apex coincide, the key angles of gear blank mainly include base cone angle, root cone angle, face cone angle, adjustment angle and cutting area angle. The relationship diagram of the above angles is shown in the figure.
In the figure:
δ B — base cone angle;
δ Angle F – cone root;
δ A — face cone angle.
It can be seen from figure 2.10 that the base cone, root cone and face cone have a common axis of rotation – oo1, and their cone vertices coincide with point o. When the (q) plane cuts the tooth blank of spiral bevel gear in the direction tangent to the base cone, (q) plane is tangent to the base cone in the straight line section OC, intersects with the root cone in the straight line sections of and og, and intersects with the face cone in the straight line sections od and OE, so as to form an angle with OC as the symmetry line ψ The adjustment area and angle are μ The cutting area. According to the geometric properties of the right triangle, the angle is adjusted next ψ And cutting area angle μ The mathematical expression is derived.
Since the base cone, root cone and face cone have a common rotation axis line oo1, and the bottom circles of the three are in the same plane, the axis oo1 is perpendicular to the bottom circle plane of the three, i.e Δ OO1C、 Δ Oo1f and Δ Oo1d is a right triangle. Since the straight line segments of and od are symmetrical to the straight line OC with the straight line segments og and OE respectively, then Δ OCF and Δ OCD is also a right triangle.
For right angles Δ Oo1c, with relation:
For right angles Δ Oo1f, with relation:
For right angles Δ Oo1d, with relation:
For right angles Δ OCF, with relation:
Combined with the formula, the adjustment angle can be obtained through the combination and simplification of the formula ψ The expression is:
For right angles Δ OCD, with relation:
Combined with the formula, the relationship formula can be obtained:
Will formula ψ The cutting zone angle can be obtained by substituting the expression into the formula and further simplifying it μ Expression for: