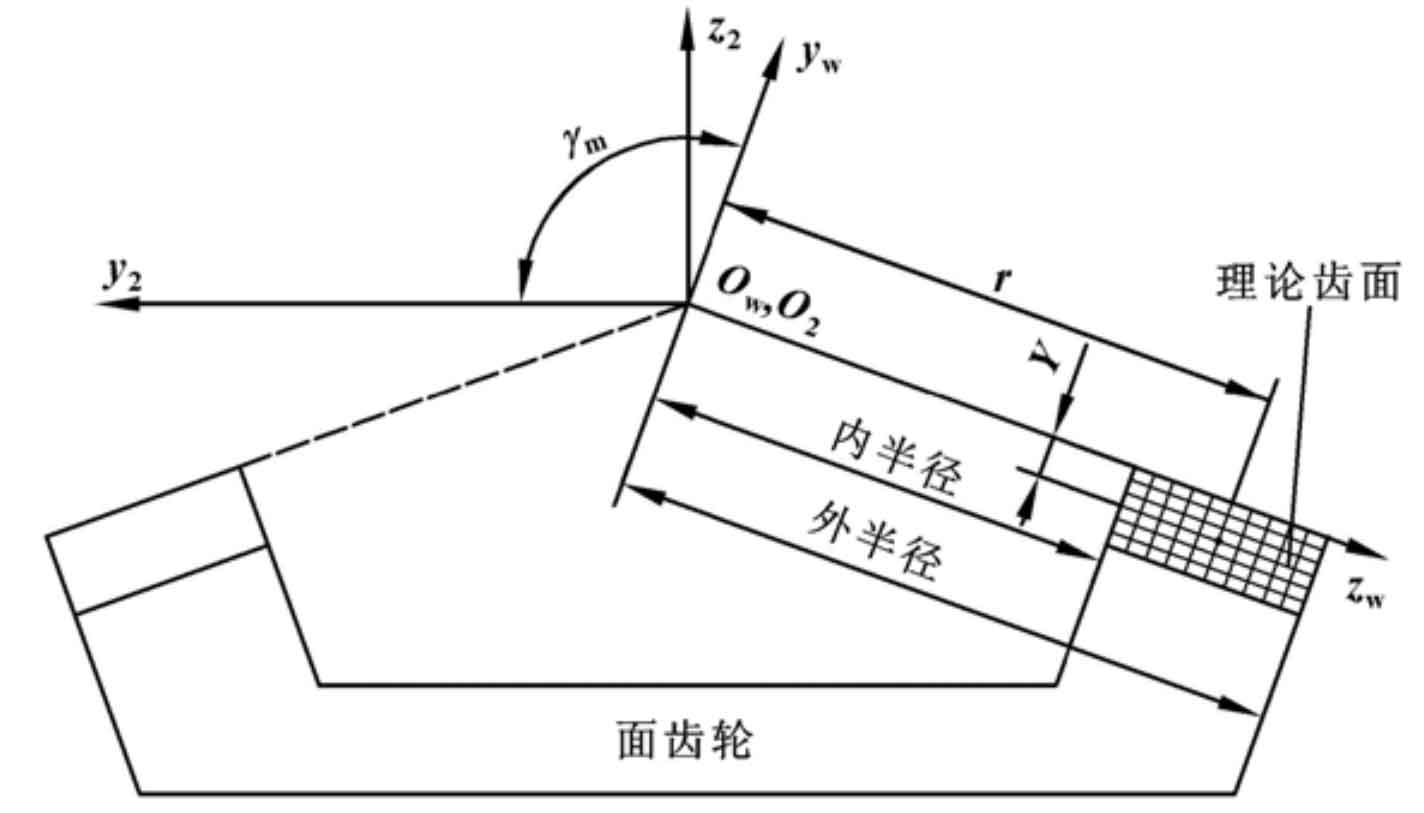
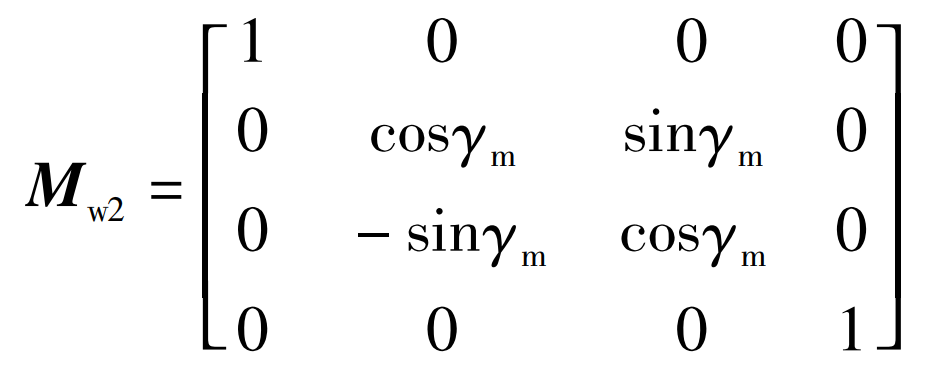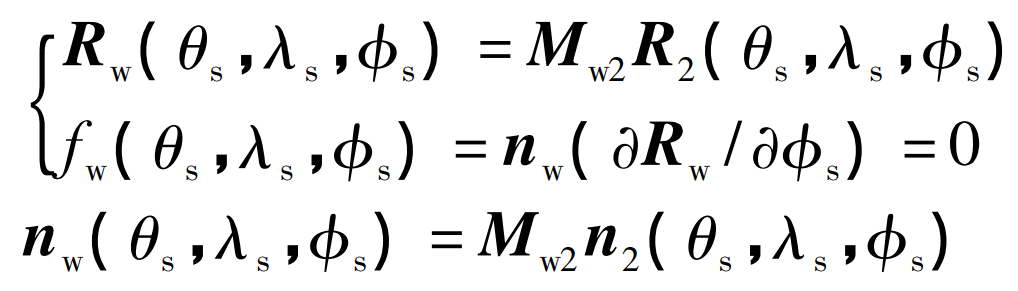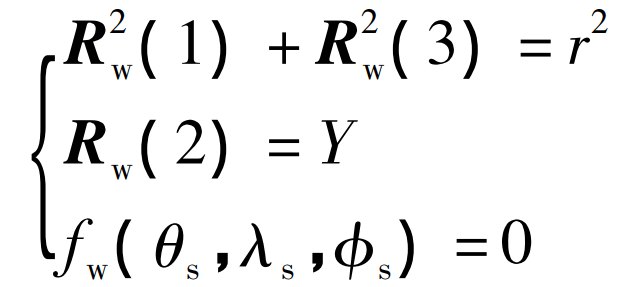The relevant parameters used are shown in the table. In order to solve the tooth surface of instant noodle gear, as shown in Fig. 1, the tooth surface of face gear is expressed in the coordinate system SW. S2 rotates counterclockwise around axis x2 γ M obtains SW, and the coordinate transformation matrix Mw2 is as follows:
In the coordinate system SW, the tooth surface equation and normal vector NW of face gear are respectively the formula:
Through the theoretical derivation of the tooth surface equation of helical offset non orthogonal face gear, it can be known that when setting the radius r of the tooth surface point of face gear and the Y coordinate of this point in the coordinate system SW, there is the following algebraic relationship:
There are three unknowns in the formula θ s、 λ s、 φ s. Three simultaneous equations can be solved θ s、 λ s、 φ The value of S is substituted into the tooth surface equation of face gear, and the coordinates of the face point of face gear can be obtained.
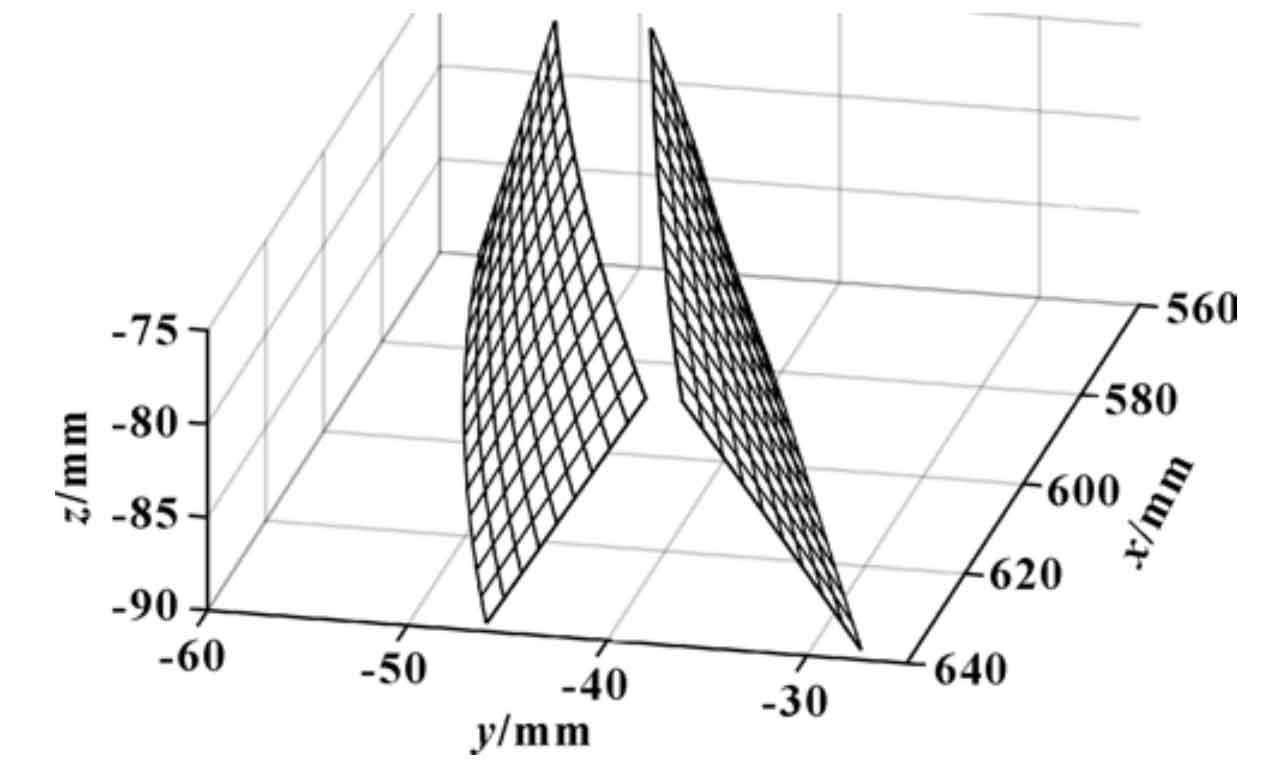
According to the relevant design parameters and the tooth surface equation of face gear, the tooth surface of face gear can be solved by compiling relevant programs with MATLAB software. The results are shown in Figure 2.