When two tooth surfaces mesh, the two tooth surfaces must be tangent at a point m in space. It can be seen that they should meet the equations:
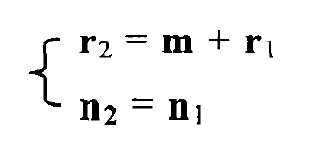
Among them, the first vector equation is the condition that the two tooth surfaces contact at point m, and the second vector equation is the condition that the two tooth surfaces are tangent at point m, which is the basic equation that all gear transmission should meet. The first equation of the differential equations can be obtained by the relative differential method:

Because:

Is the relative velocity of point m on two surfaces s (1) and S (2), so it can be written as:

We call the pair of tangents satisfying the equation on two moving surfaces a pair of conjugate directions. Obviously, only when diri / / V12 or diri is the contact line direction (DT = 0), the two conjugate directions will coincide, and the two conjugate directions will not coincide in other directions.
Let both sides of the formula be the number product of the common normal vector n of the two surfaces. Because d1r1 and d2r2 are always perpendicular to N, nd1r1 = nd2r2 = 0. In this way, the relationship v12ndt = 0 can be obtained. Except for the contact line direction DT = 0, other directions DT ≠ 0. Therefore, the two moving surfaces should also meet the conditional formula at the contact position:

The above shows that the correct meshing of the tooth surfaces of the two gears must meet the following equation:

If two moving surfaces contact along the curve determined by the meshing equation at any time, they are called line contact common roller surfaces, or completely common roller surfaces. If two moving surfaces can only contact at a certain point on the contact line at any time, they are called point contact conjugate surfaces. Both line contact common roller surface and point contact common rail surface should meet the equations when they mesh correctly at a certain point.
