In practical engineering, the stochastic response of gear nonlinear vibration is difficult to be characterized by Gaussian random process or other steady-state stochastic process, so the formula is difficult to be applied. At this time, it is more reasonable to use the weak steady-state or non-stationary bounded stochastic process. Combined with the definition, a multi pass Monte Carlo simulation method is proposed to solve such problems. The flow chart is shown in the figure. It can be seen from the figure that the proposed simulation method avoids the assumption that the nonlinear vibration response of gear transmission follows a steady stochastic process, and is more practical than the original analytical method.
In the simulation process, assuming that the number of times each vibration response exceeds the specified threshold is 0 or 1 in each time step Δ T, the judgment rules of vibration response upward or downward crossing the specified threshold are as follows:
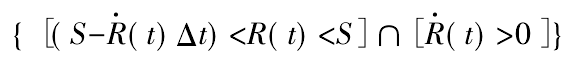
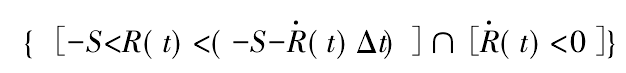
Where: s is the safety threshold of nonlinear vibration response; R (T) is the nonlinear vibration response; R · (T) is the change rate of nonlinear vibration response; Δ t is the simulation time step.
The multi pass Monte Carlo simulation method combines the applicability of the pass through rate method and the robustness of the Monte Carlo method; at the same time, combined with the reliability expression of the formula, it can make the analysis results more secure, which is conducive to the design and application of gear transmission. Based on the simulation analysis, the number of times that all kinds of vibration responses of gear nonlinear vibration exceed the specified threshold in a specified time are obtained
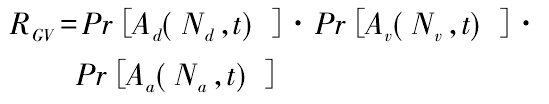
Where: Ad (nd, t), AV (NV, t) and AA (Na, t) are the random events represented by the vibration displacement, vibration velocity and vibration acceleration exceeding the specified threshold respectively; PR [AD (nd, t)], PR [AV (NV, t)] and PR [AA (Na, t)] are the probability of random events ad (nd, t), AV (NV, t) and AA (Na, t), respectively.
