Three dimensional topological modification is an effective means to improve the transmission quality of gear system, which includes two directions of tooth profile and tooth direction. The purpose of tooth profile modification is to optimize the stress distribution on the tooth surface, to make the stress distribution as uniform as possible and to reduce the peak value. The purpose of tooth profile modification is to reduce the load fluctuation, vibration and noise of the system caused by the alternation of single tooth meshing and double tooth meshing.
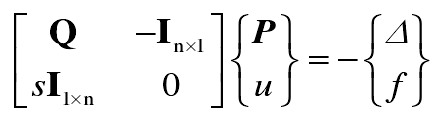
The formula is a numerical model, and its accuracy is directly related to the number of elements in the contact area. Before the modification, the rationality of mesh generation is tested. Taking the gear pair 1 of cutting section as an example, three kinds of grid cells with different densities are set in the same area around the pitch circle of gear teeth. The number of mesh cells in the tooth direction and the number of tooth profile cells are 201 × 101 (grid 1), 201 × 401 (grid 2) and 901 × 101 (grid 3), respectively. The three kinds of grids correspond to the initial cell density, mesh refinement in the direction of tooth profile and mesh refinement in the direction of tooth width.
As shown in the figure, the peak values of contact stress calculated by the three kinds of element grids are basically consistent (the relative error is 0.40%), which indicates that the mesh generation is fine enough. From the stress distribution of figures (a), (b) and (c), the stress changes of grid 1 and grid 2 in the direction of tooth width are not smooth enough, so the size setting of grid 3 is used for subsequent calculation. Along the tooth profile direction, the contact stress in the middle of the three tooth width of the mesh is extracted, as shown in the red curve in figure (c). The extracted numerical results are compared with Hertz formula, as shown in figure (d). It can be seen that due to the stress concentration at both ends of the tooth width in the numerical simulation, the stress in the middle of the tooth is slightly less than the result of Hertz formula. In addition, the numerical simulation results are in good agreement with the results of Hertz formula, which shows that the tooth surface contact model established in this study is correct.


