This article delves into the world of non – standard cylindrical gears. As industrial equipment evolves, non – standard cylindrical gears are increasingly important due to their ability to meet customized requirements. We will explore the challenges in analyzing non – standard cylindrical gears, the construction of accurate parametric models, and methods for verifying and optimizing the models. Through in – depth research, this paper aims to provide a comprehensive understanding and practical guidance for the design, analysis, and application of non – standard cylindrical gears.
1. Introduction
1.1 The Significance of Non – standard Cylindrical Gears
In the realm of modern mechanical engineering, gear 传动 (gear transmission) is a fundamental mechanism that enables the transfer of power and motion. Standard cylindrical gears have long been the go – to choice in many applications due to their well – defined characteristics and ease of production. However, with the continuous development of industrial equipment, the need for gears that can adapt to specific operating conditions has grown. Non – standard cylindrical gears, which can be customized in terms of pressure angle, addendum, dedendum, displacement coefficient, and other parameters, have emerged as a crucial solution. They offer a broader application prospect as they can be tailored to meet the unique requirements of various industrial scenarios, such as in precision machinery, aerospace, and automotive manufacturing.
1.2 Challenges in Analyzing Non – standard Cylindrical Gears
The modification of parameters in non – standard cylindrical gears leads to changes in tooth shape and tooth root transition curves. These changes, in turn, affect the tooth surface bearing capacity, tooth root bending stress, and transmission performance. Current evaluation methods face significant limitations. The first method, which relies on ISO standard gear equivalent empirical formulas, provides only rough estimates. It fails to accurately capture the complex relationships between non – standard parameters and gear performance, and the results are often of low accuracy and difficult to adjust according to parameter changes. The second method, involving the use of three – dimensional software for modeling and analysis, is extremely cumbersome. It requires a series of complex steps including solving the tooth profile curve mathematical model, creating a 3D model, and setting up various conditions in finite element software. Moreover, when parameters change, the entire modeling process needs to be redone, which is time – consuming and inefficient.
2. Construction of Non – standard Cylindrical Gear Accurate Parametric Model
2.1 Key Components of the Tooth Profile
The tooth profile of a gear consists of two main parts: the involute part and the transition curve part. For external meshing gears, the tooth profile is typically generated by a rack cutter (such as a hob or worm – gear grinding wheel) cutting method. In this case, the transition curve is an extended involute. For internal meshing gears, the tooth profile is formed by the gear shaping process, and the transition curve is an extended epicycloid. Calculating the coordinates of points on the involute part is relatively straightforward. However, accurately calculating the coordinates of points on the transition curve and ensuring their proper connection with the involute part is a key challenge. This is achieved by formulating calculation equations that simulate the generation process, which is essential for obtaining the coordinates of the entire tooth profile.
2.2 Building the Tooth Profile Equation
2.2.1 Tooth Profile Equation for Hobbing External Gears
When hobbing a spur gear, as shown in Figure 1 (please insert a figure here showing the geometric relationship of hobbing a spur gear), LM represents the straight – line part of the rack cutter edge, and MN is the rounded – off part at the cutter edge end with the center of the rounded – off part being Q. We establish a fixed rectangular coordinate system XPY and a coordinate system \(X_{1}O_{1}Y_{1}\) on the rack cutter. The rolling pitch line is set on the \(O_{1}X_{1}\) axis and coincides with the fixed axis PX, while the \(O_{1}Y_{1}\) axis bisects the tooth space of the cutter. During the gear – hobbing process, the \(X_{1}O_{1}Y_{1}\) coordinate on the rack cutter moves to the left, and the \(O_{1}X_{1}\) axis moves along the fixed axis PX. Let the center of the gear being processed be \(O_{2}\), and P be the meshing node between the rack cutter and the gear. The radius of the pitch circle of the gear is \(O_{2}P\). When hobbing, the pitch circle of the gear and the rolling pitch line of the rack cutter perform pure rolling.
Based on the geometric relationships, the coordinates of the tooth profile cutting point B can be derived as follows (although we avoid complex math formulas in the text, the equations are presented in a more descriptive way here): The position of the rack cutter in the coordinate system is related to several parameters. The \(x_{1}\) coordinate of the cutting point B is influenced by factors such as the displacement coefficient \(\xi\), the module m, the pressure angle \(\alpha_{0}\), and the distance S from the \(O_{1}Y_{1}\) axis of the rack cutter to the fixed coordinate PY axis. Similarly, the \(y_{1}\) coordinate is also determined by these parameters. For the rounded – off part of the cutter edge, as shown in the local enlarged view of Figure 1b (please insert the corresponding local enlarged figure), with the radius of curvature of the rounded – off part of the cutter edge being \(R_{T}\), we can calculate the distance from the starting point M of the rounded – off part to the rack center line and the distance from the curvature center Q to the rolling pitch line. Through geometric relationships, we can further obtain the coordinates of the rounded – off cutting point K. Finally, by transforming the coordinates of the cutting points B and K of the cutter tooth profile to the coordinate system of the gear being processed, we can determine the coordinates of the tooth profile and the transition curve.
| Parameter | Symbol | Explanation |
|---|---|---|
| Rack module | m | A fundamental parameter determining the size of the gear teeth |
| Displacement coefficient | \(\xi\) | Adjusts the position of the tooth profile along the radial direction |
| Rack pressure angle | \(\alpha_{0}\) | Affects the force transmission direction and tooth – meshing characteristics |
| Distance from \(O_{1}Y_{1}\) axis to PY axis | S | Determines the relative position of the rack cutter in the coordinate system |
| Radius of curvature of the rounded – off part of the cutter edge | \(R_{T}\) | Influences the shape of the tooth root transition curve |
2.2.2 Tooth Profile Equation for Shaping Internal Gears
The profile of an internal gear is generated by the gear shaping cutter. To obtain an accurate internal gear profile, we first need to understand the generation process of the gear shaping cutter profile. Assume that the gear shaping cutter profile is processed by a rack. As shown in Figure 2 (please insert a figure showing the generation process of the gear shaping cutter profile), we define the coordinate systems \(S_{1}(x_{1}, y_{1})\) and \(S_{j}(x_{j}, y_{j})\) which are fixed to the gear shaping cutter and the machine frame respectively.
Point \(P_{1}\) is the meshing node when the rack processes the gear shaping cutter profile. We can derive the equation of the gear shaping cutter profile curve through geometric and kinematic analysis. However, the gear shaping cutter profile often has a sharp corner at the tooth tip, which can cause stress concentration at the tooth root of the internal gear ring formed by the gear shaping cutter. Therefore, we replace the sharp – corner part with a rounded – off arc \(M_{1}N_{2}\) to improve the strength of the internal gear ring. To determine the equation of the rounded – off curve at the tooth tip of the gear shaping cutter, we first need to find the center \(Q_{1}\) of the rounded – off arc \(M_{1}N_{2}\). By using the geometric properties of the normal lines of the gear shaping cutter profile curve and the tooth tip circle, we can find the intersection point of two normal lines, which is the center \(Q_{1}\) of the rounded – off arc. Then, we can obtain the coordinates of the cutting point \(K_{1}\) of the rounded – off part at the tooth tip of the gear shaping cutter in the coordinate system \(S_{1}(x_{1}, y_{1})\).
Finally, through coordinate transformation between the cutter coordinate system and the workpiece coordinate system, we can derive the involute equation and the transition curve equation of the internal gear tooth profile. The involute equation of the internal gear tooth profile is related to parameters such as the pitch circle radius \(r_{p1}\) of the gear shaping cutter, the displacement coefficient \(x_{1}\), the pressure angle \(\alpha_{1}\), and the number of teeth \(Z_{1}\) and \(Z_{2}\) of the gear shaping cutter and the internal gear. The transition curve equation also takes into account parameters such as the radius of the rounded – off part \(r_{T1}\) at the tooth tip of the gear shaping cutter and the angle \(\psi_{1}\).
| Parameter | Symbol | Explanation |
|---|---|---|
| Pitch circle radius of the gear shaping cutter | \(r_{p1}\) | Determines the size of the gear shaping cutter’s pitch circle |
| Displacement coefficient of the gear shaping cutter | \(x_{c}\) | Adjusts the tooth profile of the gear shaping cutter |
| Pressure angle at the pitch circle of the gear shaping cutter | \(\alpha_{1}\) | Affects the meshing characteristics of the gear shaping cutter |
| Number of teeth of the gear shaping cutter | \(Z_{1}\) | Influences the shape and size of the gear shaping cutter |
| Number of teeth of the internal gear | \(Z_{2}\) | Determines the size and meshing relationship of the internal gear |
| Radius of the rounded – off part at the tooth tip of the gear shaping cutter | \(r_{T1}\) | Improves the strength of the internal gear by modifying the tooth tip shape |
2.3 Parametric Model Building
2.3.1 Building Parametric Elements
According to the tooth profile curve equations derived above, we can write corresponding programs. By setting the required number of grids, we can evenly divide and accurately calculate the coordinates of discrete points on the end face of non – standard internal and external cylindrical gears. As shown in Figure 4 (please insert a figure showing the discrete nodes on the end face of single teeth of internal and external gears), we can obtain the discrete nodes on the end face of single teeth of internal and external gears.
Based on these discrete nodes, referring to the natural point sorting method of elements given in the ABAQUS manual, we can build a finite – element mesh model of a single tooth of non – standard internal and external gears. By rotating and arraying the single – tooth model along the circumferential direction and merging the tolerance, we can obtain the full – tooth finite – element model. In ABAQUS, the choice of element type has a significant impact on the accuracy and efficiency of simulation calculations. Since the 2 – order finite – element mesh element may cause oscillations of the equivalent nodal contact force between angular nodes, resulting in inaccurate judgment and verification of the contact state, we use the linear reduced – integration element (C3D8R) in this paper. This element has accurate calculation results when solving for displacement and is less affected by grid distortion. After precisely assembling the established finite – element model, setting materials, analysis steps, reference points, contact pairs, field variables, historical variables, boundary conditions, and loads, and then solving, we can obtain result files such as contact stress at different meshing positions on the tooth surface and relative rotation angles between teeth.
2.3.2 Setting up the Parametric Finite – Element Model
To avoid repetitive operations, we convert repetitive work into platform – specific languages to achieve parametric settings and solutions. ABAQUS provides two parametric methods. The first method uses a script file and relies on the Python language. Python is a language oriented to the graphical user interface (GUI), which can realize the automatic reproduction of operations. It contains execution commands for each step. The second method is implemented through an Inp file, which uses the Fortran language directly oriented to the model itself. The Inp file contains information such as model data, material properties, contact properties, analysis step settings, loads, and boundary conditions. The first method has a stronger ability to achieve automation, while the second method requires operators to have a deeper understanding of the ABAQUS software platform language. The author has implemented the parameterization of both algorithms according to the syntax rules. After comparison, the first method was selected. The specific process of the parametric method is shown in Figure 8 (please insert a figure showing the two parametric methods in ABAQUS).
3. Verification of Model Accuracy
3.1 Verification Example Selection
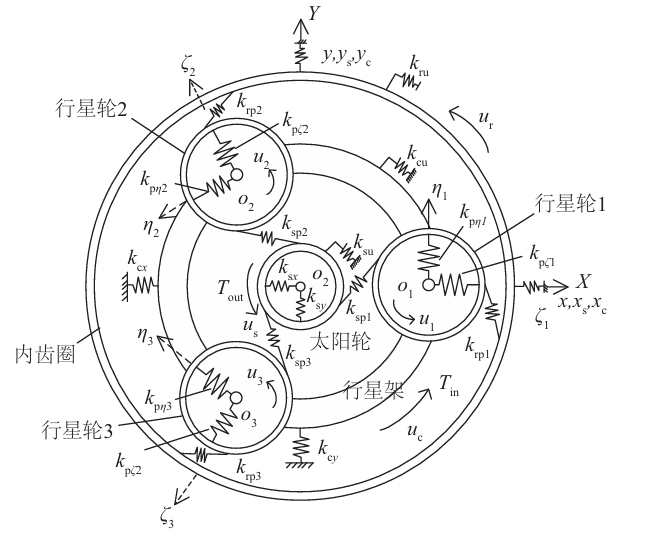
To verify the accuracy and feasibility of the established model, we take a non – standard planetary transmission system as an example. This system contains internal and external meshing pairs, which can be used to analyze and verify non – standard cylindrical gear internal and external meshing pairs. The relevant parameters of the planetary transmission system are shown in Table 1.
| Parameter | Sun Gear | Planet Gear | Internal Gear Ring |
|---|---|---|---|
| Number of Teeth | 48 | 55 | 162 |
| Module /mm | 3.8 | 3.8 | 3.8 |
| Pressure Angle /(°) | 22.5 | 22.5 | 22.5 |
| Tooth Width /mm | 90 | 88 | 88 |
| Sun Gear Rotational Speed /(r/min) | 1128.0 | – | – |
| Input Power /kW | 2985.8 | – | – |
| Input Torque /(N▪m) | 25278.7 | – | – |
| Single – Path Meshing Force /N | 60003.2 | – | – |
3.2 Comparison of Tooth Surface Contact Stress Before and After Modification
To fully verify the accuracy of the non – standard cylindrical gear parametric analysis model established above, we take the parabolic micro – modification with high – precision requirements as an example for comparison. Figures 9 – 12 (please insert figures showing the comparison of tooth surface contact stress before and after modification for external and internal meshing) show the comparison of tooth surface contact stress before and after modification. In addition, Figures 11 and 12 also show the comparison of tooth surface contact stress before and after tooth surface modification when there is a shaft – angle error of 1′ in the non – standard gear. Through comparison and verification, it is found that the parametric model established in this paper is accurate and efficient, which can provide technical support for non – standard gear parameter design, process adjustment, and tooth modification.
4. Optimization of Non – standard Cylindrical Gear Performance
4.1 Influence of Parameter Adjustment on Gear Performance
Based on the established parametric model, we can explore the impact of adjusting parameters such as pressure angle, addendum, dedendum, and displacement coefficient on gear performance. For example, increasing the pressure angle can improve the force – transmission capacity of the gear, but it may also increase the tooth root bending stress. Adjusting the displacement coefficient can optimize the meshing performance and tooth – load distribution. By systematically studying the relationship between parameters and performance, we can find the optimal parameter combination to meet specific design requirements.
4.2 Tooth Modification Strategies for Performance Enhancement
Tooth modification is an important means to improve the performance of non – standard cylindrical gears. In addition to the parabolic micro – modification mentioned above, other modification methods such as profile crowning and lead crowning can also be used. Profile crowning can reduce the edge contact of the tooth surface during meshing, improving the contact stress distribution. Lead crowning can compensate for errors in the alignment of the gear axis, reducing the vibration and noise during gear operation. By applying these tooth – modification strategies based on the parametric model, we can further enhance the performance of non – standard cylindrical gears.
5. Conclusion
In this article, we have comprehensively studied non – standard cylindrical gears. Through the simulation of the tool and processing process of non – standard internal and external gears, based on differential geometry and meshing principles, and using spatial coordinate transformation methods, we have accurately established the tooth profile curve equations of non – standard internal and external gears. Combining with the secondary development technology of ABAQUS software, we have achieved the construction of parametric finite – element models of non – standard internal and external gears. Through the verification of tooth surface contact stress characteristics before and after modification of non – standard internal and external meshing pairs, we have demonstrated the accuracy and efficiency of the established model. This model ensures the complete consistency between the theoretical tooth surface mathematical model and the actual tooth surface (excluding errors), effectively guaranteeing the reliability of contact simulation results. Moreover, based on this model, we can accurately apply modification parameters, assembly errors, processing errors, etc. to the corresponding tooth surface grid nodes, constructing real tooth surfaces and complex – modified tooth surfaces. This provides a powerful technical means for non – standard cylindrical gear parameter design, process adjustment, and tooth modification, promoting the development and application of non – standard cylindrical gears in various industrial fields.