The finite difference method is used to solve the two temperature equation. The laser pulse width is 800 FS, and the depth step along the beam direction is 1 nm and the time step is 1 FS. The initial condition is that the temperature of electron and lattice is 300 K before ablation. Boundary conditions: the electron temperature and lattice temperature of the substrate before and after ablation are 300 K. By solving the two temperature equation and taking different energy density, we can get the variation law of the surface temperature field of 20CrMnTi material ablated by femtosecond laser.
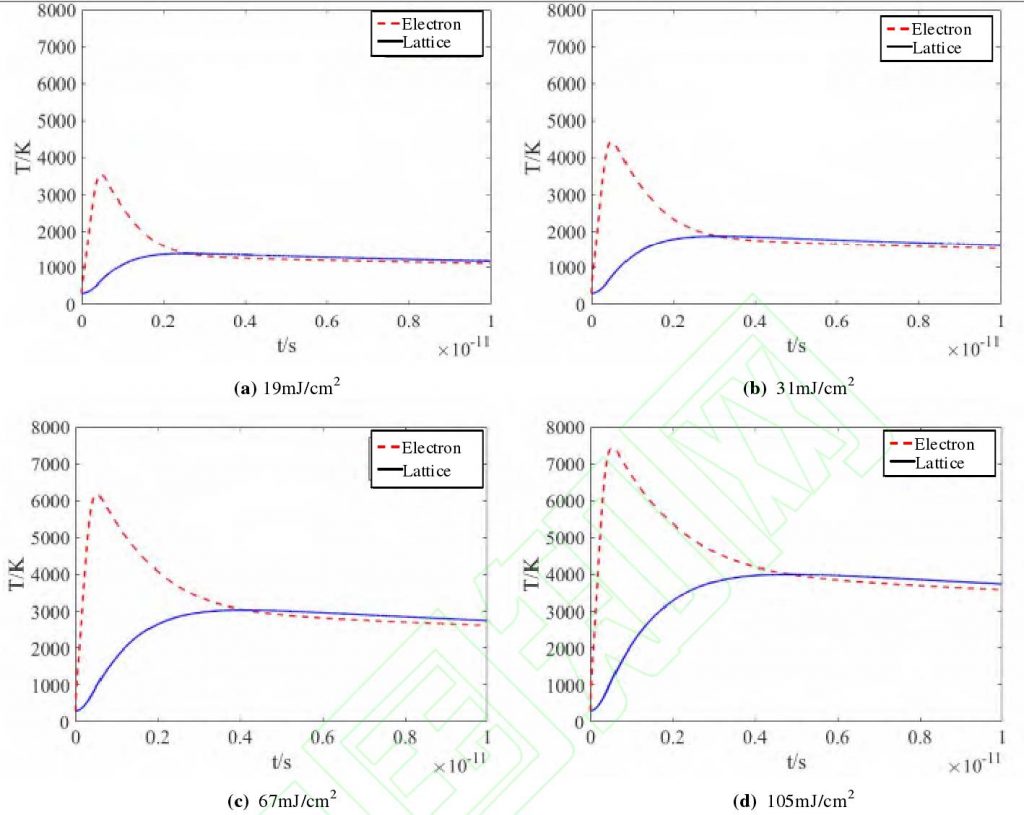
As shown in Fig. 1, after the temperature of the electronic system reaches the peak temperature, the laser energy absorbed by the electronic system is transferred to the lattice system of the gear material through the effect of electro acoustic coupling. At this time, the temperature of the electronic system decreases gradually due to the thermal diffusion, and the temperature of the lattice system increases gradually due to the absorption of energy. After that, the two systems tend to thermal equilibrium. The whole non-equilibrium process of energy coupling is completed at about 10 PS.
When the energy density is 19 MJ / cm2, as shown in Fig. 1 (a), the peak temperature of the electronic system after 0.48 PS is about 3550 K. The temperature of the two systems tends to be thermal equilibrium after 2.3 PS, and the equilibrium temperature is about 1400 K. when the melting temperature of the crystal lattice is not reached, the material is not ablated.
When the energy density is 31 MJ / cm2, as shown in Fig. 1 (b), the peak temperature of the electronic system after 0.50 PS is about 4500 K. The temperature of the two systems tends to be thermal equilibrium after 3.2 PS, and the equilibrium temperature is about 1850 K, reaching the melting temperature of the lattice. At this time, the gear material begins to melt, and part of the material changes from solid to liquid and vaporizes.
When the energy density reaches 67 MJ / cm2, as shown in Fig. 1 (c), the peak temperature of the electronic system after passing 0.52 PS is about 7500 K. after the equilibrium temperature of the two systems is 3.9 PS, it tends to the thermal equilibrium state, and the equilibrium temperature is about 3100 K. When the temperature of the lattice is reached, the lattice material can be vaporized rapidly or plasma eruption can be formed under high temperature and high pressure. Part of the absorbed energy in solid or liquid state can be quickly transformed into gas state, and the material removal efficiency is high.
When the energy density reaches 105 MJ / cm2, as shown in Fig. 1 (d), the temperature of the two systems tends to thermal equilibrium state after 4.6 PS. at this time, the equilibrium temperature is about 4050 K, which is much higher than the melting temperature and gasification temperature of gear material, and the material removal efficiency is higher than the first three kinds of energy. However, with the increase of energy density, the relaxation time required for the equilibrium between the electron and the lattice temperature increases, and the lattice temperature decreases slowly when the lattice temperature reaches the maximum value. Because the transmission speed of heat energy in the electron is much faster than that in the lattice, the electron temperature in the equilibrium state is slightly lower than the lattice temperature.
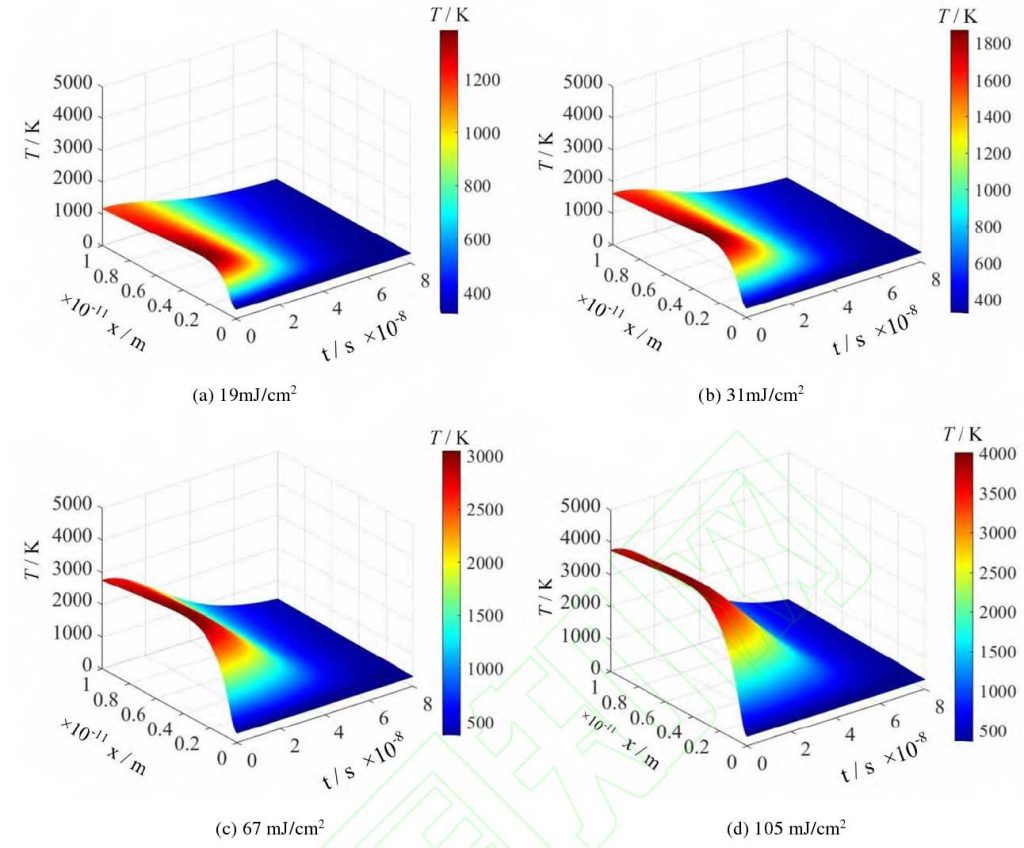
The three-dimensional temperature distribution of the lattice system under different energy densities of 19 MJ / cm2, 31 MJ / cm2, 67 MJ / cm2 and 105 MJ / cm2 are simulated respectively. The results are shown in Fig. 2. It can be seen that when femtosecond laser ablates the surface of gear material, the lattice temperature is related to time and transmission depth. The lattice temperature increases with the increase of energy density and decreases along the depth direction. Along the direction of the laser beam, material removal occurs in the lattice region with a depth of more than 40 nm, and the material is not ablated in the lattice area below 40 nm. Therefore, the ablation of femtosecond monopulse only occurs on the surface of the material, and the effect on the interior of the material is not obvious.
