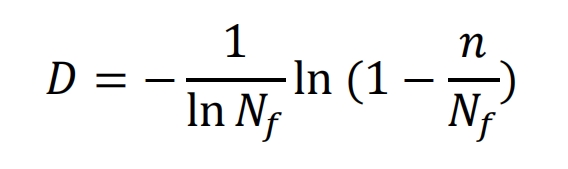The variation of bending stress on the tooth root during traction of subway vehicles is significant, so establishing a widely applicable and convenient calculation model for predicting the bending fatigue life of helical gears is of great significance. In the field of engineering, a fatigue life prediction model based on Palmgren Miner cumulative damage theory is commonly used to predict the fatigue life of structures. In order to accurately predict the bending fatigue life of helical gears, a combined method of helical gear bending fatigue testing and finite element simulation is used to calculate the energy accumulation curve of the tooth root under different stress amplitudes. Based on the energy accumulation curve, obtain the fracture accumulation energy curve under different stress amplitudes. Based on the above curve and Palmgren Miner linear cumulative damage theory, establish a prediction model for the bending fatigue life of helical gears.
1. Linear cumulative damage theory
In today’s engineering applications, the Palmgren Miner cumulative damage theory is the most widely used. This theory considers the fatigue damage of helical gears generated at each stage of the mechanical structure to be independent of each other, thus achieving linear accumulation. When the accumulation value reaches the threshold, the fatigue damage of helical gears occurs. Therefore, the fatigue life of helical gears can be inferred based on the accumulated damage. According to Palmgren Miner’s cumulative damage theory, the fatigue damage of helical gears under constant amplitude loading is:
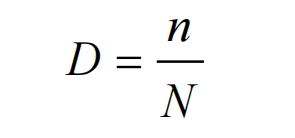
When subjected to multi-level loading, the damage caused by different stress sizes can be linearly superimposed to obtain the total damage D, which is expressed as:
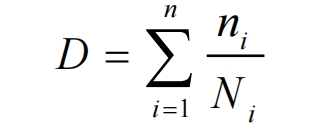
In the formula: D represents damage; Ni represents the number of cycles of the helical gear under various loads; Ni represents the fatigue life of helical gears under various loads.
When the total damage is superimposed to the critical value of damage, fatigue failure of helical gears occurs, and the number of load cycles in this process is called the fatigue life of helical gears. The Miner theory is easy to apply, and its damage critical value is generally 1. However, based on a large amount of experimental data analysis, the critical value of fatigue damage in helical gears may deviate far from 1, generally not exceeding the range of three times. To improve the accuracy of predicting the fatigue life of helical gears, the critical value of fatigue damage can be modified so that it is not taken as 1, but rather an empirical value. This theory is called the Relative Miner Theory. All actual engineering structures are subjected to different load spectra, and the life prediction results based on Miner theory often have significant errors that cannot be ignored. Compared to Miner theory, this error can be reduced and made widely accepted.
The specific measures are as follows:
(1) Design helical gears based on actual working conditions;
(2) Obtain the fatigue life test value Nt based on the helical gear fatigue test;
(3) Calculate the cumulative damage based on the linear accumulation of damage and predict the fatigue life to obtain the predicted value Na;
(4) The ratio of the fatigue life test value Nt of helical gears to the predicted fatigue life value Na is defined as the critical damage value.
The core idea of the above theoretical methods is similar, and the linear cumulative damage theory is widely used in engineering practice due to its simple construction and fewer material parameters.
2. Nonlinear helical gear fatigue cumulative damage model
A large number of experts and scholars have proposed various nonlinear cumulative damage theories and methods based on the mutual influence between loads, material physical performance degradation, energy criteria, and other aspects to address the defects in the fatigue cumulative damage model of linear helical gears.
(1) Carten Dolan model
The Carten Dolan model, which considers the interaction between loads and can effectively describe the fatigue behavior of helical gears under variable amplitude loads, has been increasingly valued and applied by people. Its definition of damage is:
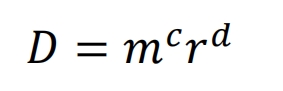
In the formula, m is the number of material damage nuclei, r is the damage growth rate, and c and d are the material constants. The damage caused by n cyclic loads is:
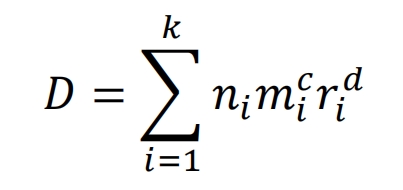
According to the Carten Dolan theory, the structure fails after the fatigue damage of the helical gear reaches a critical value. This theory assumes that the total damage caused by fatigue failure of structural helical gears is a constant value, so the following equation can be derived:
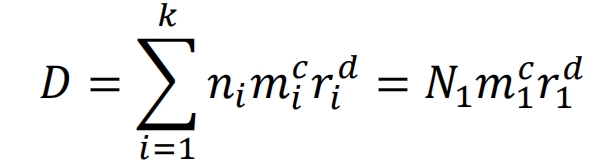
Under constant amplitude load, N1 represents the fatigue life value of the helical gear under this stress; Under variable amplitude load, N1 is the fatigue life value of the helical gear corresponding to the maximum load.
Because fatigue damage to helical gears persists and continues to accumulate, there is mi=m1, and the formula can be changed to the following:
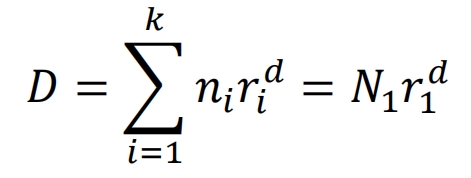
Therefore, the fatigue life of helical gears based on the Carten Dolan theory is calculated using the following formula:
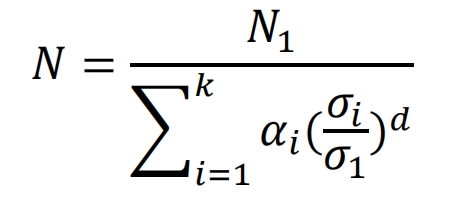
In the formula, 𝛼 is the ratio of the number of cycles under the action of stress 𝜎; K is the stress level; D is the material constant. Based on the fatigue test data of helical gears, Dolan and Carten suggest taking 4.8 for high-strength steel d and 5.8 for other d.
(2) Nonlinear cumulative fatigue damage model for helical gears based on material toughness dissipation
According to the theory of cumulative fatigue damage in helical gears, the damage variables can be defined by selecting physical parameters of materials such as strength, stiffness, energy, and toughness. Scholars such as Ye Duyi analyzed the toughness dissipation law and fatigue damage evolution law of materials, and verified through experimental processes that the change in toughness can be used as a variable for fatigue damage of helical gears. They proposed a nonlinear fatigue cumulative damage model based on material toughness dissipation. Through extensive experimental research, it has been found that the change in material toughness is very significant during the fatigue failure process of helical gears. Based on this, scholars such as Ye Duyi believe that the damage caused by a single cycle can be expressed as toughness:
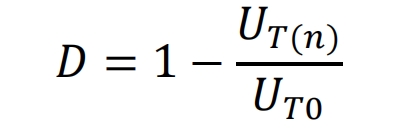
In the formula, UT0 is the toughness of the material in its initial state, and U T (n) is the remaining toughness of the material after n load cycles. Analyzing a large amount of experimental data, the evolution equation of material toughness can be expressed as follows:
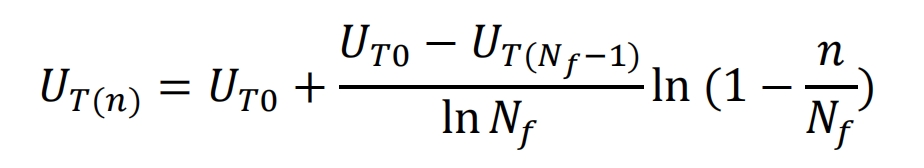
By substituting the formula, the evolution equation of nonlinear fatigue cumulative damage can be obtained:
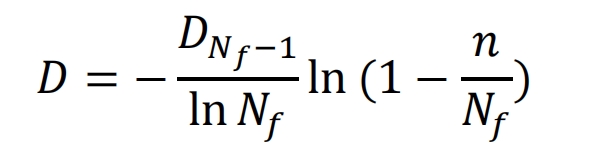
In the formula, DNf-1 is the accumulated damage value of the material after experiencing Nf-1 load cycles, which can be regarded as the occurrence of helical gear fatigue failure when the accumulated damage reaches DNf-1. After analyzing the experimental results, it is believed that the value of DNf-1 can be taken as 1. Therefore, the formula can be expressed as: