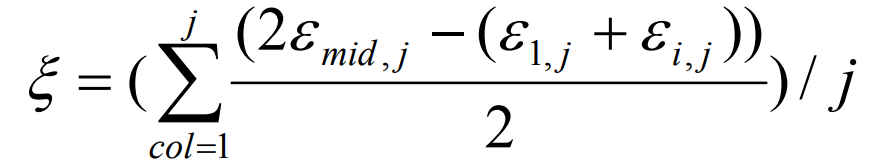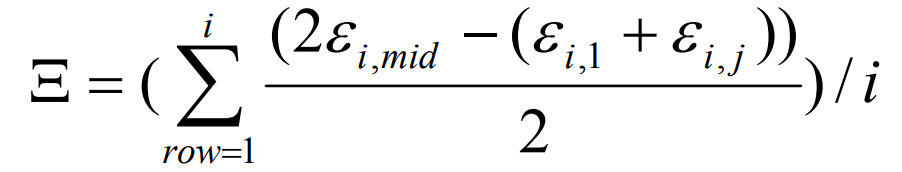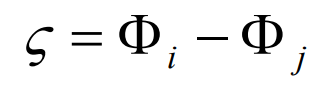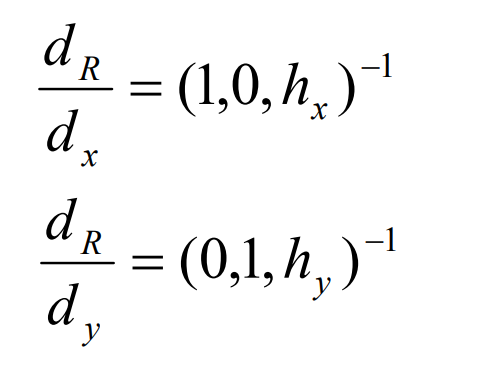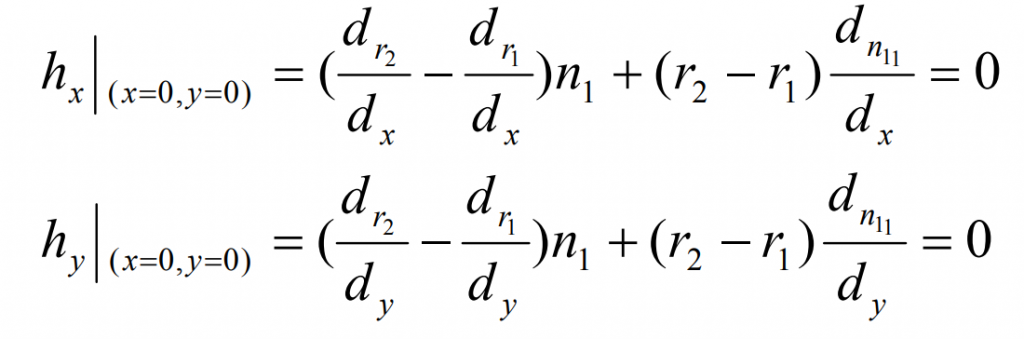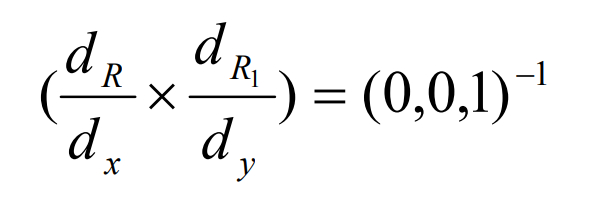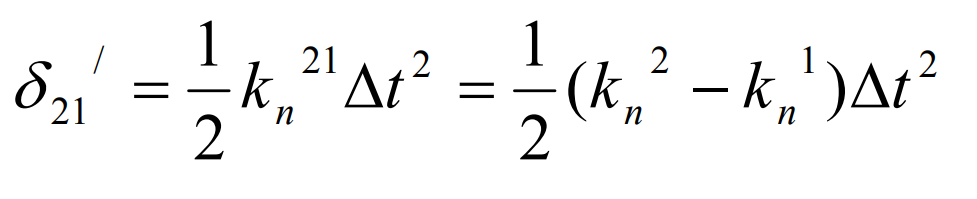The second-order error of logarithmic spiral bevel gear can be understood as the longitudinal and transverse drum shape error of tooth surface. It adopts the form of saddle, that is, the distortion error of difference surface. We can use the average tooth curvature error, average drum shape error and distortion error for quantitative evaluation.
Average tooth curvature error:
Average drum error:
The distortion error is:
Where:
I – data serial number of transverse measuring points on the tooth surface;
J – serial number of longitudinal measuring point data on vertical tooth side;
Mid – serial number of measurement data points of transverse midpoint or longitudinal midpoint of tooth surface;
ε i. J – error value of tooth surface at measuring point (I, J);
Xi, J – distance between measuring points along the tooth surface;
Yi, J – distance between measuring points on the side of vertical tooth.
Suppose the surfaces Σ 1 and Σ The tangent point of 2 is m, the XY plane is taken as the tangent plane of m point, and the coordinate origin is m point. Derive the formula from X and y to obtain:
Derive the formula and find the derivative value of point m:
The normal vector of point m on the difference surface can be obtained by substituting the formula into the formula and making the vector product:
It can be seen from the above formula that the normal vector of point m is perpendicular to the XY plane. If point m is the coordinate origin and the XY plane is the tangent plane of the difference surface, then at point m Σ 1 Σ 2. The unit normal of the sum difference surface coincides. By Σ 1 Σ 2 the normal section of the topological surface formed by the difference of normal curvature at point m along any tangent direction is:
Where kn1 and kn2 are Σ 1 and Σ 2 respectively Σ 2 normal curvature at point M.
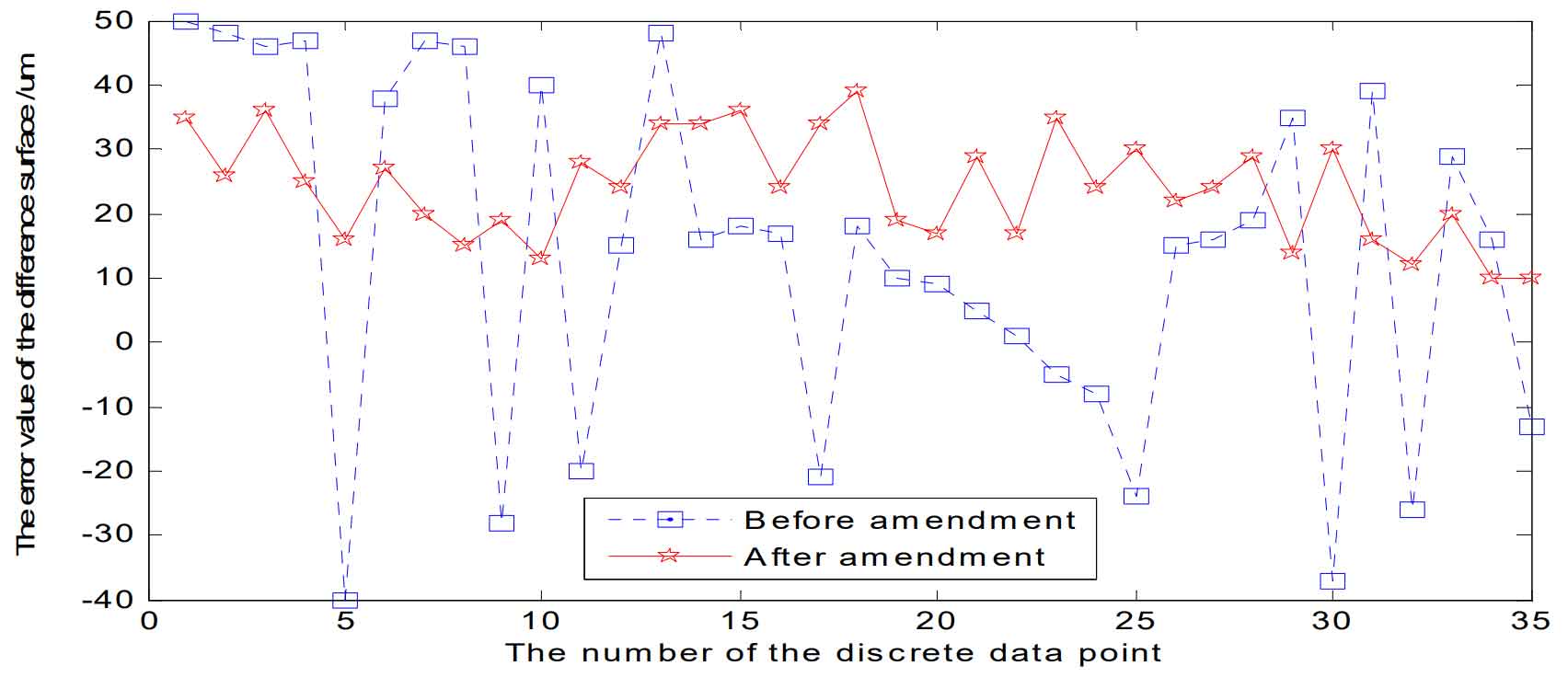
For the difference surface equation of logarithmic spiral bevel gear, the coefficient A0 of order 0 is the comprehensive reflection of measurement error and pitch error, which is described by the pitch error of logarithmic spiral bevel gear; The first-order coefficient is related to the helix angle and pressure angle of the logarithmic spiral bevel gear, which quantitatively describes the error of the average pressure angle and average helix angle of the whole tooth surface of the logarithmic spiral bevel gear; The logarithmic mean curvature error and the logarithmic mean curvature error of the spiral surface of the gear describe the tooth profile error of the gear. x. Y is the main direction of the design reference point along the theoretical tooth surface. In order to reflect the error of the whole tooth surface, take 5 and 7 × Grid data points are used as a reference. As shown in the figure, the correction result curve of tooth surface deviation of logarithmic spiral bevel gear is shown. It is obvious that the error after correction is small. Before correction, the maximum deviation is 55um and the minimum deviation is – 40um; After correction, the maximum deviation is 43um and the minimum deviation is 10um, which achieves the expected ideal effect.