Abstract
In this study, a novel approach utilizing power skiving technology for the machining of double-circular-arc internal gear is proposed to address the current challenges of difficulty, poor accuracy, and low efficiency encountered in conventional processing methods. A mathematical model is established based on the principle of power skiving, and the simulation of the double-circular-arc tooth profile formation is conducted using Vericut software. The cutting forces during the power skiving process are simulated and analyzed using Abaqus, and their dependence on various machining parameters is investigated. Experimental validation is performed on a six-axis CNC machine tool, and the spiral accuracy of the machined gears is evaluated to confirm their compliance with design specifications. This research not only enhances the processing technology of double-circular-arc gears but also improves the machining accuracy and efficiency of internal gear, thereby laying a solid foundation for future investigations into double-circular-arc internal meshing and planetary transmissions.
1. Introduction
Double-circular-arc gears, known for their superior load-bearing capacity, improved lubrication, and compact design suitable for high-torque applications in confined spaces, present new opportunities for mechanical equipment such as oil rigs and drilling machines. However, traditional manufacturing methods for double-circular-arc internal gear, primarily relying on gear shaping, suffer from limitations in machine performance and processing efficiency, resulting in difficulties, poor accuracy, and low productivity. To overcome these challenges and promote the practical application of double-circular-arc planetary transmissions, innovative machining techniques are urgently needed.
This paper explores the potential of power skiving technology for the efficient and precise manufacture of double-circular-arc internal gear. Power skiving, an efficient gear cutting method that integrates hobbing and shaping processes, offers high tooth surface accuracy and material removal rates. By simulating and experimentally verifying the feasibility of this approach, we aim to expand the processing capabilities for double-circular-arc gears and enhance their overall manufacturing quality.
2. Literature Review
The existing methods for internal gear processing can be classified into three main categories: form cutting, non-instantaneous envelope cutting, and generative cutting. Form cutting utilizes a cutter with a profile identical to the tooth space, suitable for large-modulus spur gears but requiring post-processing due to significant deviations. Non-instantaneous envelope cutting, where the cutter profile does not fully match the tooth space, generates the tooth shape through the envelope of the cutter’s continuous trajectory, resulting in complex cutting motions. Generative cutting, including shaving, shaping, and power skiving, utilizes the meshing motion between the cutter and workpiece for high-precision tooth profile generation.
While shaving and shaping processes are limited by low efficiency and specialized equipment requirements, power skiving emerges as a promising alternative. Previous studies have focused on power skiving for external gears, with a few investigations extending to face gears. However, little attention has been paid to double-circular-arc internal gear, necessitating further research in this area.
3. Mathematical Model for Double-Circular-arc Internal Gear Power Skiving
3.1 Principles of Power Skiving
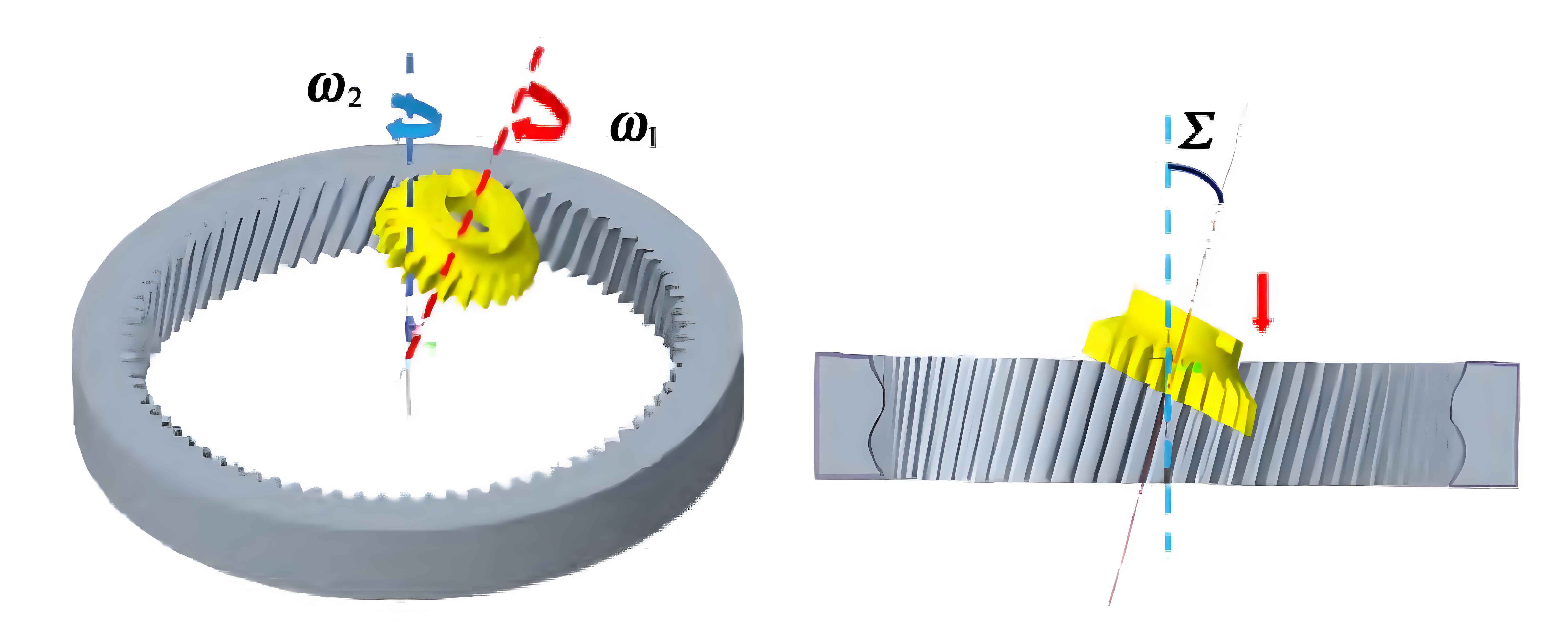
Power skiving involves a spatial intersection between the centers of the workpiece and cutter, as illustrated in Figure 1. The axis intersection angle (Σ) between the cutter and workpiece is defined by the difference in their helix angles (β1 for the cutter and β2 for the workpiece):
Sigma=∣β1−β2∣
The center distance (a) between the cutter and workpiece is given by:
a=r2−r1
where r2 and r1 are the pitch circle radii of the internal gear and cutter, respectively.
During machining, the cutter rotates at an angular velocity ω1, the workpiece rotates at ω2 in the same direction, and a feed motion at velocity v1 along the workpiece axis occurs. The angular velocities and feed speed must satisfy the relationship:
omega1=i21ω2−r1cosβ1sinβ2⋅v1
3.2 Coordinate System and Mathematical Model
The coordinate systems for the double-circular-arc internal gear power skiving process are shown in Figure 2. The transformation matrix between the workpiece motion coordinate system S2 and the cutter motion coordinate system S1 is given by:
begin{bmatrix} x_1 \\ y_1 \\ z_1 \\ 1 \end{bmatrix} = M_{10}M_{0p}M_{p2} \begin{bmatrix} x_2 \\ y_2 \\ z_2 \\ 1 \end{bmatrix}
where M10, M0p, and Mp2 are the respective transformation matrices.
By substituting the tooth surface equation of the workpiece into the above transformation, the tooth profile in the cutter coordinate system can be obtained. This profile, along with the cutter tooth surface equation, forms the basis for subsequent simulation and experimental validation.
4. Simulation of Double-Circular-arc Tooth Profile Formation
4.1 Simulation Setup
Based on the machine tool configuration, a three-dimensional model for power skiving is established in Figure 3. The toolpaths are determined by the X, Y, Z, and W axes, controlling the cutter motion and workpiece displacement. The U and V axes facilitate rotation of the cutter and workpiece, respectively.
Using a straight-toothed cutter with 24 teeth and an internal gear with 76 teeth, a helix angle of 20° for the internal gear, and a cutter speed of 50 rpm (corresponding workpiece speed of 15.1315 rpm), the simulation is initialized with a feed rate of 0.01 mm/min along the workpiece axis.
4.2 Simulation Results
The simulated tooth profile formation process is presented in Figure 4, resulting in a double-circular-arc tooth profile consistent with the national standard GB/T 12759—1991, as shown in Figure 5. A comparison of the simulated and theoretical tooth profiles in Figure 6 confirms the high accuracy of the simulation, with minor overcutting observed at the transitional arc regions.
5. Simulation of Cutting Forces during Power Skiving
5.1 Simulation Methodology
The cutting force simulation is performed using Abaqus’s explicit analysis module. The cutter and workpiece models, shown in Figure 8, are assembled according to the power skiving kinematics. Mesh refinement is applied to the cutting edge region of the cutter and the workpiece contact area, with element sizes of 0.5 mm for the cutter and 0.1 mm for the workpiece to accurately capture the dynamic interactions.
5.2 Simulation Results
The cutting forces Fz (main cutting force), Fy (radial force), Fx (feed force), and the resultant force Fn are monitored during the simulation. The variation of these forces over time is plotted in Figure 11, while the stress distribution at different simulation steps is presented in Figure 10.
5.3 Sensitivity Analysis
An L9(34) orthogonal array is employed to investigate the influence of cutting parameters (cutter speed, feed rate, and cutting depth) on the maximum resultant cutting force. The analysis reveals that the feed rate has the most significant impact, followed by cutter speed and cutting depth (Table 3).
6. Experimental Validation and Accuracy Assessment
6.1 Experimental Setup
The experimental validation is conducted on a YK2260MC six-axis CNC machine tool using a硬质合金钢S390 cutter with a surface coating and a hardness of 66 HRC. The machining parameters are summarized in Table 4, with a multi-pass cutting strategy employed for both roughing and finishing operations.
6.2 Experimental Results
The machined double-circular-arc internal gear is presented in Figure 13, demonstrating the feasibility of power skiving for this gear type. The gear’s spiral accuracy is evaluated using a 650GMA gear measuring center, with results shown in Figure 15 and summarized in Table 5. All measured parameters meet or exceed the design specifications, confirming the high precision of the power skiving process.
7. Conclusion
This study presents a comprehensive investigation into the power skiving of double-circular-arc internal gear, encompassing mathematical modeling, simulation, experimental validation, and accuracy assessment. Key findings include:
- The Vericut simulation successfully reproduced the target double-circular-arc tooth profile, providing a solid foundation for experimental machining.
- The sensitivity analysis identified the feed rate as the most influential factor governing cutting forces, with significant implications for optimizing machining parameters.
- Experimental results demonstrated the high efficiency and precision of power skiving for double-circular-arc internal gear, with measured spiral accuracies exceeding design requirements.
Future work could focus on further refining the cutting tool design and exploring adaptive control strategies to mitigate tool wear and improve surface finish.
