According to the characteristics of pitting metal shedding, the most intuitive performance after pitting is that the width of meshing contact line becomes shorter, which can be known from the expression of time-varying meshing stiffness (gear tooth stiffness and contact stiffness) of gear. When the mesh contact line width decreases, for contact stiffness, the width of the contact tooth becomes shorter, which affects its stiffness change; for gear tooth stiffness, the sectional area and moment of inertia at the meshing action line decrease, which affects its stiffness change. In order to study the effect of pitting erosion on stiffness, a general mathematical model for calculating mesh stiffness under pitting erosion characteristics was proposed based on the analysis theory.

Rectangles (Fig. 1 (a)) were still selected to simulate the geometric features of pitting pits, and the gear end face and section were expanded and analyzed, as shown in Fig. 2. In the xoy plane, the boundary of pitting pits is X∈ [Xs_st, Xs_ed]. Based on the boundary [Xs_st, Xs_ed] and the expansion diagram of zoy plane within the range, the position relationship of rectangular pits in the zoy plane can be determined by parameters Ls, ws and hs. In order to facilitate model calculating unification and generalization, the boundary of the rectangular pit position all through the function form to express, because of the cross section, with symmetry rectangular pit position in Ls + ws / 2 ≤L / 2 or less and a Ls + ws / 2 ≥L / 2 or two under the condition of the cross-sectional area and moment of inertia changes with symmetry, so stiffness model for single point corrosion pit, only need to study the Ls + ws / 2 ≤L / 2 or less under the condition of meshing stiffness changes.

Firstly, the cross-sectional area is calculated. Under the condition of LS + WS /2≤L/2, the mathematical function of the rectangular pit can be expressed as:

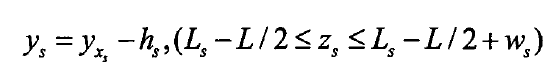
Then, the area of the rectangular pit, As, is derived by numerical integration, and its expression is As follows:

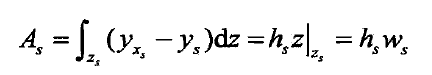
Then it can be deduced that the cross-sectional area at the engagement point Xs, Axs, is:

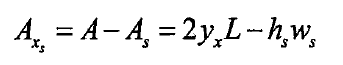
According to the geometrical properties of the plane figure, the moment of inertia under the pitting etched section was analyzed and calculated. Firstly, the centroid of the section was calculated according to the static moment. The detailed derivation process was as follows:

The barycenter of rectangular pitting pits is the formula. Since the section under lossless conditions is relative to the Z axis and the Y axis, the corresponding barycenter is the origin of the coordinate (0,0). The centroid of the section under pitting corrosion can be deduced according to the calculation formula of the centroid coordinate of the combined figure, as shown in the formula.

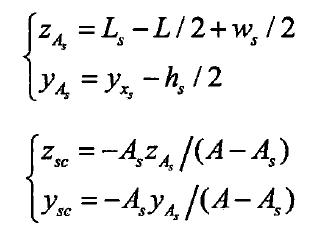
According to the parallel shift axis theorem, the moment of inertia of the pitting cross section with respect to centroid ZSC axis can be calculated as:

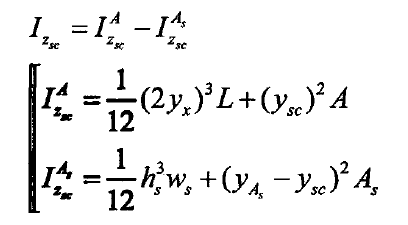
The contact tooth width under rectangular pitting can be expressed as:

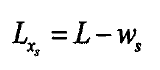
To pitting corrosion pit border for X ∈ [Xs_st Xs_ed] cross-sectional area and moment of inertia and contact tooth width length respectively into gear tooth stiffness and contact stiffness calculation formula related to the calculation of time-varying mesh stiffness, stiffness formula after the substitution, in order to reduce the repetitive writing, to simplify the formula expression, only account segmentation effect with stiffness calculation.

Combined with the pitting stiffness formula and the gear matrix stiffness formula, the time-varying mesh stiffness calculation formula of the formula was substituted to study and analyze the mesh stiffness under the action of pitting corrosion.