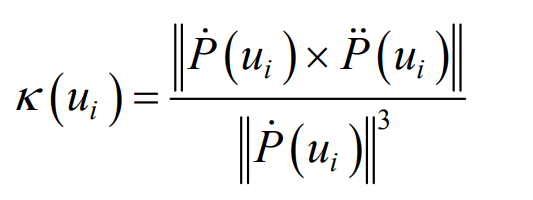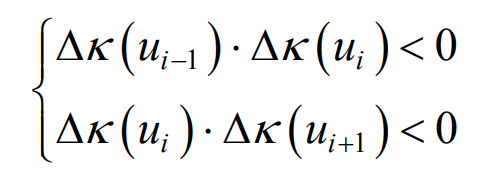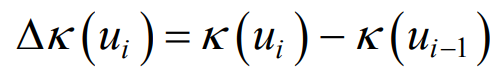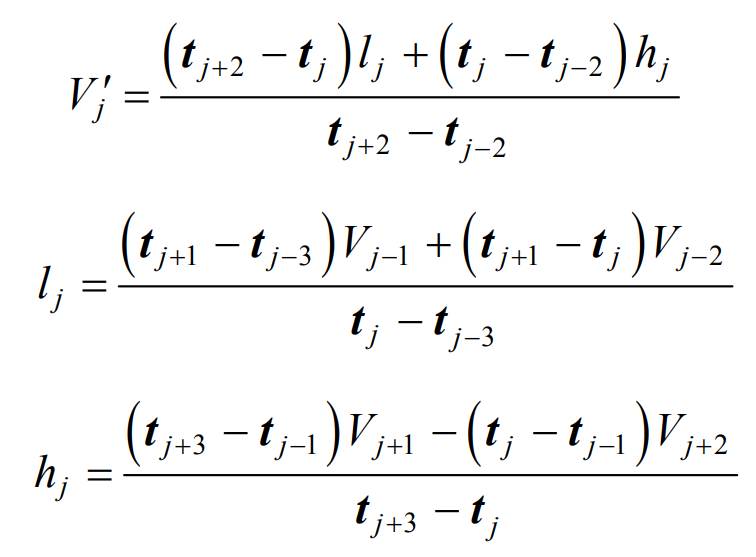The traditional discrete data fairing algorithm is based on the curvature calculation of interpolation curve, and the “noise points” are deleted to achieve the purpose of surface fairing. This method can not guarantee the retention of discrete data points in the wear area of hypoid gear tooth surface. To solve this problem, the traditional fairing algorithm is improved to improve the fairing of surface on the premise of preserving discrete data points.
Curvature of type value point P (UI) corresponding to control vertex VI:
Where, P. (UI) is the first derivative of P (UI) to UI; P. (UI) is the second derivative of P (UI) to UI.
The formula is used to solve the curvature of the type value point corresponding to a control vertex, and the “noise point” is judged by the change of the curvature difference of the type value point. If the curvature of the type value point P (UI) corresponding to the control point VI satisfies the formula, it is judged as “noise point”.
Where:
After judging the “noise point”, in order to achieve the purpose of preserving the “noise point” and realizing discrete data smoothing, the “noise point” moving algorithm is studied. Note that the control point VJ is the judged “noise point”, the node vector corresponding to VJ is J T, and the new control vertex v ‘J satisfying the smoothing condition is:
The formula can be used to smooth the discrete data points of hypoid gear tooth surface, and combined with the previous local interpolation method, the construction effect of hypoid gear tooth surface can be greatly improved.