As shown in Figure 1, P is the initial meshing point of the non-circular gear, O1 and O2 are the rotation centers of the two non-circular gears respectively. Given O1O2 = a, let o1p = R1, o2p = R2, φ 2 is the rotation angle of the driven non-circular gear

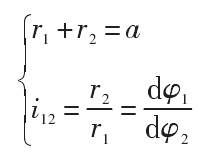
It can be deduced from the formula that:

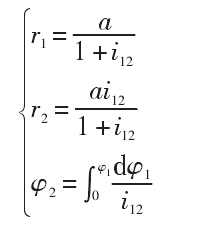
By substituting the formula, we can get:

From the formula, as long as you know φ We can find R1, R2 and R1 φ 2。 When using MATLAB programming, the φ 1 is defined as from 0 to 2 π The number of elements in the array is n (the larger the value of n is, the higher the calculation accuracy is, take n = 2) × 104）； According to this principle, R1, R2 and R2 can be obtained φ The number of elements in each array is also n. Due to array φ There is a functional correspondence between 1 and array R2, and the array φ 1 and array φ If there is a function corresponding relationship between R2 and R2, then the array R2 and the array R2 are the same φ There is also a corresponding functional relationship between R2 and F, that is, R2 = F（ φ 2) 。 It is not necessary to solve the function f, and the interpolation method can be used according to the known function F φ 2 solve R2 or known R2 solve φ 2。

The expressions of pitch curve of driving non-circular gear (x1, Y1) and driven non-circular gear (X2, Y2) are as follows:

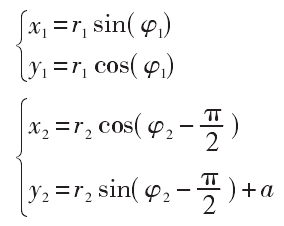
The pitch curve of non-circular gear as shown in Figure 2 is obtained by solving the above equation, which is also the initial rotation position of non-circular gear.