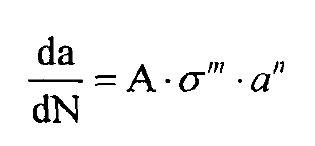The fatigue fracture process of metal materials can be divided into three stages: crack initiation, propagation and instantaneous fracture. In the first stage, when Δ K> Δ At kth, the fatigue crack does not propagate; When Δ K≈ Δ At kth, DA / dN < 10-7mm / cycle, where Δ Kth is called the threshold stress of fatigue crack propagation, which is a kind of material
Two important fatigue performance parameters. The first stage of fatigue crack initiation often occurs on the surface or internal defects of metal materials, such as knife marks on the machined surface or internal defects or inclusions. The stress concentration factor in these areas is large, which causes uneven plastic deformation and then forms microcracks. In the second stage, the fatigue crack growth rate DA / DN is generally 10-6-10-2mm / cycle. The experimental study shows that DA / dN at this stage- Δ K shows a good linear relationship in the double logarithmic coordinate system. In the third stage, DA / dN increases nonlinearly with the increase of crack length, and the material breaks quickly. Generally, the fatigue life of this stage is not considered. Therefore, the fatigue failure process of metal parts in engineering mainly refers to the fatigue crack propagation stage. The research on the fatigue crack growth behavior in the second stage began in the late 1940s. At that time, the expression for calculating the fatigue crack growth rate was given as follows:
Where, σ I. applied stress, N; α – crack length, mm; A. M, N – constant determined by experiment.
The stress intensity factor is introduced to describe the singularity of stress and strain at the crack tip, which lays a foundation for the prediction of fatigue life by linear elastic fracture mechanics. In the 1960s, Paris and Erdogan applied the theory of fracture mechanics to put forward Paris formula:
Where, Δ K – amplitude of stress intensity factor, C and N need to be determined by experiment.
Paris formula shows that the control parameter (driving force) of fatigue crack growth is the amplitude of stress intensity factor Δ K。 Although Paris formula is only applicable to the steady-state crack growth zone (the second stage), it provides theoretical guidance for subsequent research. After 1970s, the threshold stress of fatigue crack propagation was proposed Δ Kth or critical stress intensity factor amplitude.