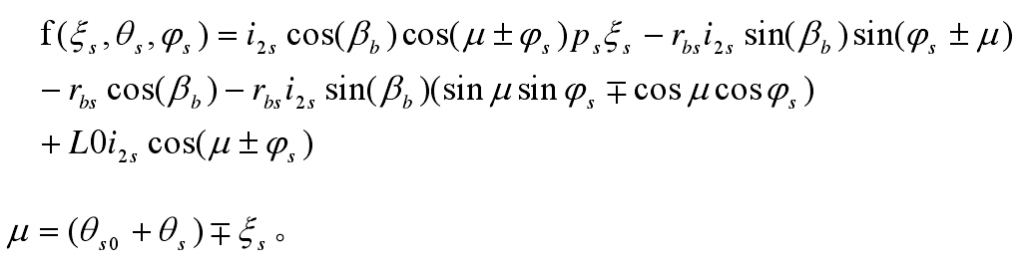Before deriving the equation of helical gear, the meshing equation is obtained first. The process of machining helical gear is similar to the meshing process of two spatial gears. In order to derive the meshing equation, vs is expressed in the dynamic coordinate system ss by using the dynamic coordinate system ss of the tool gear. The speed vector of the tool relative to the face gear is:
From the derivation and calculation:
Where w (s) s and w (2) s in the tool coordinate system SS represent the angular speed of tool rotation and the angular speed of helical gear rotation respectively. RS represents the vector of any meshing point on the tool when the tool engages with the face gear. γ M is the intersection angle of the two transmission shafts, and its value is 90 °, l0 is the distance between the coordinate origin OA and OM of the two coordinate systems.
Assuming that the tool rotates at unit angular speed, there are:
Relationship between w (s) s and w (2) s:
Where I2S is the transmission ratio between face gear and cutter.
Sorting out the formula:
According to the knowledge of gear meshing principle, the meshing equation of two gear surfaces is obtained:
Substituting the formula into, the expression of meshing equation is derived:
The tooth surface of the tool is expressed in the coordinate system S2 through coordinate transformation to form a follow-up motion ϕ S-varying surface group. From the transformation relationship between coordinate system SS and coordinate system S2, the tooth surface equation of helical gear is deduced:
In the formula, the matrix [m2, S] analyzes the relationship between the tool gear coordinate system and the face gear coordinate system from the figure, and deduces that the conversion matrix [m2, S] between the coordinate systems is as follows: