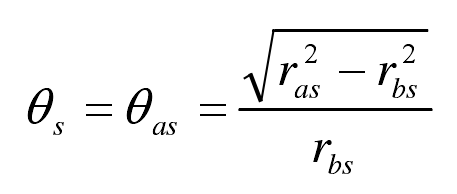When the helical gear meshes with the tool, the speed of the former at the contact point is zero. At this time, undercutting phenomenon will occur on its tooth surface, and undercutting boundary line will appear on the tool tooth surface. In order to find out the minimum inner radius of helical gear without undercutting at the tooth root, s at the intersection of undercutting limit on the tooth surface of the tool and the top circle of the tool is used θ Value. Then there are:
The conditions under which undercutting does not occur on the tooth surface of helical gear during generation are as follows:
Expand the above formula to obtain the parameters ϕs 、 θs and ξs Relationship between:
The nonlinear equations are solved by successive approximation method, and the parameters are solved ϕ S and ξ The value of S. Substitute its value into the tooth surface equation of helical gear and calculate the corresponding coordinates x * 2 and y * 2 to obtain the minimum inner radius of helical gear without undercutting during machining: