The double-input-single-output helical gear transmission system under asymmetric load has become an important structure in the important power propulsion device of large ships due to its advantages of high power density, compact structure and flexible power parameter ratio. However, due to the particularity of the structure, with the improvement of the power, the helical gear at the low load end changes from the following power consumption to the active power, which means that the connected helical gear pair has a state switch from back meshing to positive meshing, and the nonlinear instability phenomena such as gear tooth collision, vibration, noise and so on will occur, which will affect the safe and stable operation of the propulsion system. Therefore, considering various nonlinear factors that affect the stability of the system, establishing a typical dynamic model of the double-input-single-output helical gear transmission system and studying the influence of asymmetric dynamic parameters on the vibration characteristics of the system are the key to scientifically explain the instability mechanism and suppress the occurrence of instability.
For the dynamic modeling of helical gear system, many research results have been produced. According to the different degrees of freedom of the system, pure torsion model, bending-torsion coupling model, bending-torsion – pendulum coupling model and bending-torsion – pendulum – axis coupling model have appeared successively. In the 1980s, Iida et al. studied the dynamic characteristics of helical gear meshing by establishing a bend-torsion coupling model of helical gear system; Kahraman comprehensively considered the translation and swing characteristics of the helical gear-rotor in two orthogonal directions in the plane perpendicular to the shaft, and established the bend-torsion-swing coupling vibration model of the helical gear-rotor system; With the in-depth study of the coupling system, Eritenel et al. established the bend-torsion-shaft-pendulum coupling model of helical gears respectively, and carried out the finite element analysis and experimental method research of dynamic characteristics.
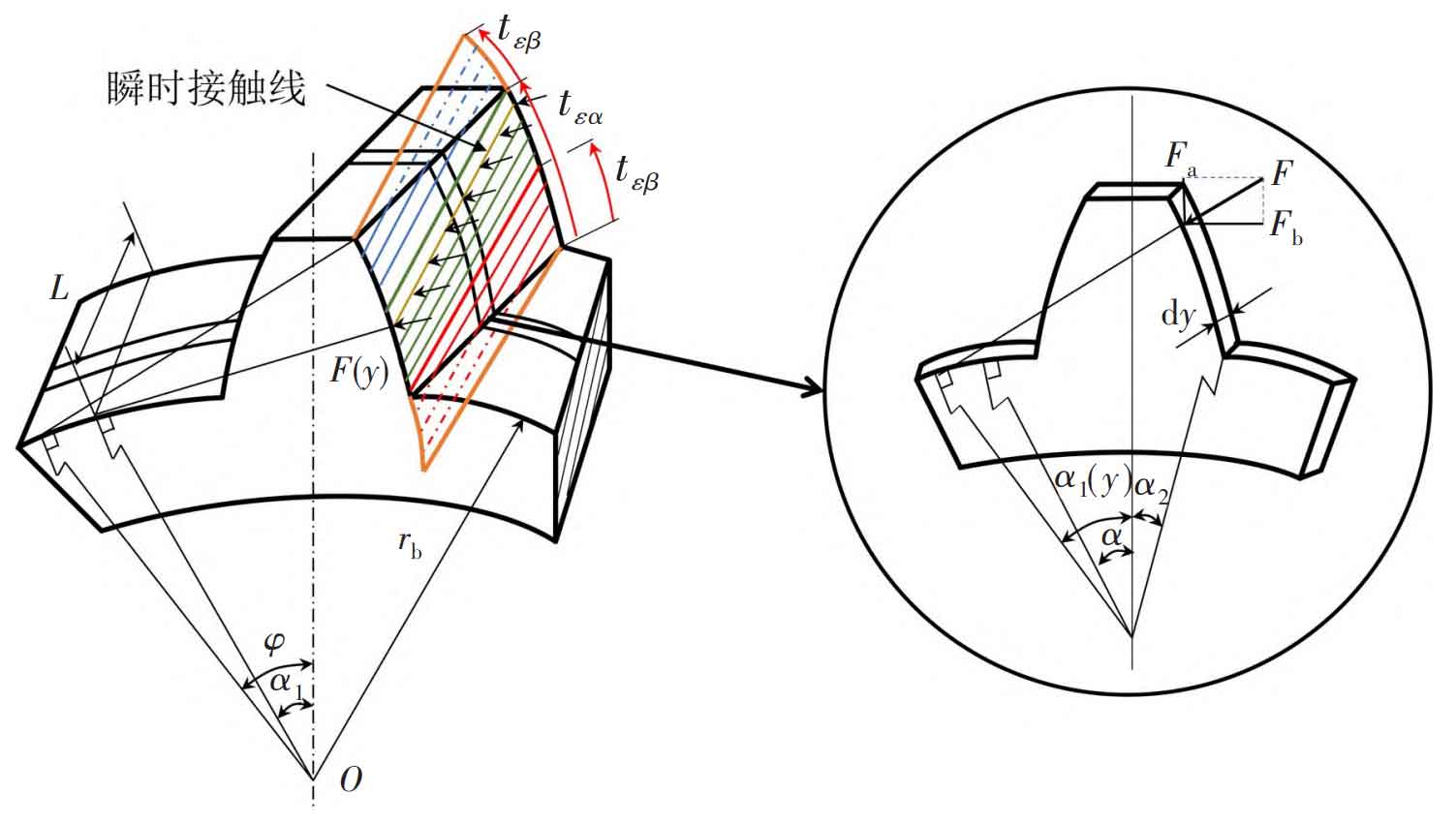
The internal excitation generated by the gear tooth meshing itself and the external excitation generated by other factors of the system are the key factors affecting the stability of the system operation. Feng et al. deduced the calculation method of time-varying meshing stiffness of helical gears by slice method, and compared the calculation results with the finite element method; Guilbault et al. studied the nonlinear meshing damping of single-degree-of-freedom spur gear, and provided an empirical formula calculation method; Liu Zhansheng and others further considered the influence of elastic shaft and unbalance mass, established the dynamic model of helical gear and rotor coupling system, and carried out experimental research; Ristivojevi ć The model of non-uniform load distribution along the contact line based on the minimum elastic potential energy is proposed, and the calculation formula of time-varying load distribution coefficient along the action line is obtained; Gao established a dynamic model of the parallel drive system of double spur gears considering the stiffness of the oil film support, and studied the effect of the phase difference of the meshing stiffness of the two driving helical gears on the vibration. There are also many in-depth research results on the evolution of dynamic characteristics of helical gear system with internal parameters.
Yang Shaopu et al. studied the nonlinear dynamics of spur gear system by using the incremental harmonic balance method, and obtained the influence law of system parameters on amplitude frequency characteristics; By analyzing the bifurcation characteristics of helical gear rotor system under internal and external excitation, Cui Yahui and others studied the influence of support stiffness and backlash on the vibration characteristics near the critical speed of the system; Li Yinong et al. considered the meshing force of helical gear, the meshing force of spline coupling and the nonlinear contact force of bearing, and studied the influence of the meshing frequency, the number of rollers and the bearing clearance on the vibration characteristics of the gear rotor-bearing system.
Although the double-input-single-output parallel helical gear structure is widely used in the power propulsion system of large ships, the research on its dynamic characteristics is rare, and the mechanism of instability under asymmetric dynamic parameters is still unclear. On the basis of considering the time-varying meshing stiffness, meshing stiffness phase difference, nonlinear backlash, meshing damping, comprehensive meshing error and other parameters of the helical gear, the dynamic model of the double-input-single-output helical gear system is established, and the evolution law of the vibration characteristics of the system with the asymmetric dynamic parameters is studied, and the mechanism of system operation instability is clarified.
