Abstract
Accurate analysis of the meshing misalignment of the spiral bevel gear transmission system under load is the basis for the optimal design of the gear tooth profile. When the transmission shaft structure is complex, the beam element model is used to solve the large deformation difference of the shaft, which will lead to an inaccurate analysis of the meshing misalignment of the gear pair. In order to solve this problem, this paper proposes a meshing misalignment analysis method for the step-by-step spiral bevel gear transmission system based on the solid finite element method. Firstly, the finite element model of the transmission shaft is established, and the bearing stiffness is coupled to the transmission shaft. Secondly, apply the equivalent gear pair meshing force on the gear shaft to analyze the shaft deformation. Then, combined with the deformation of the active and passive gear shafts, the meshing misalignment of the gear pair is analyzed. Finally, considering the meshing misalignment state of the gear pair, the finite element model of the loading contact analysis of the gear teeth is constructed, and the meshing mark offset and transmission error change of the gear pair are analyzed. The method is compared with the full finite element analysis model of the transmission system, including gears, shafts, and bearings. It shows that the meshing misalignment state of the gear pair analyzed by this method is in good agreement with the full finite element model, and the analysis efficiency is significantly improved.
1. Introduction
Spiral bevel gear is core transmission components widely used in equipment such as vehicles, aircraft, and ships. During the power transmission process, the deformation of the transmission system under load can lead to an offset in the meshing state of the gear pair, affecting the transmission performance of the gear pair [1]. Usually, the tooth surface design and modification are carried out in combination with the meshing misalignment results of the gear pair. Therefore, rapidly and accurately analyzing the meshing misalignment of the transmission system is very important for evaluating the loaded meshing performance of the gear pair and optimizing the tooth surface design.
Scholars at home and abroad have conducted extensive research on the analysis methods for the meshing misalignment of gear transmission systems. Wang Qin et al. [2] established a coupled analysis model of a multi-support shafting system, comprehensively considering the effects of bearing stiffness, gears, shafts, and housings to solve the gear meshing misalignment, and verified it through experiments. Gao Jie et al. [3-4] comprehensively considered the influence of the support deformation of the casing, shafting, and bearings on the offset of the gear axis, and superimposed the equivalent misalignment to modify the tooth surface of the spiral bevel gear. Qin Qiuxia et al. [5-6] established a meshing misalignment calculation model considering the machining errors of the casing and the interference fit of the bearings, and designed the tooth surface of the spiral bevel gear based on the calculation results, verifying the meshing mark and transmission error after meshing misalignment through experiments. Lai Changfa et al. [7-8] used Masta software to establish a simulation analysis model of the drive main reducer to calculate the meshing misalignment of the spiral bevel gear and compared the simulation analysis results with experiments. However, to obtain calculation results quickly, the above studies mostly simplify the transmission shaft to a beam element model when analyzing the shaft deformation. This simplification ignores the assumptions derived from Euler-Bernoulli beam and Timoshenko beam theories. When the transmission shaft structure is complex, the deformation analysis results may have large errors, leading to inaccurate calculations of the meshing misalignment of the gear transmission system and affecting the optimization design effect of the tooth surface.
To address the above issues, this paper proposes a step-by-step meshing misalignment analysis method for spiral bevel gear transmission systems based on the solid finite element method. This method considers the influence of bearing stiffness and gear meshing force and adopts the solid finite element model for the deformation analysis of the transmission shaft to ensure the accuracy of the meshing misalignment calculation of the gear pair. Based on this, a loading contact analysis of gear teeth considering the influence of meshing misalignment is established to significantly improve the calculation and analysis efficiency.
2. Calculation of Meshing Misalignment of Gear Pair
2.1 Definition of Meshing Misalignment
The gear transmission system includes components such as shafts, bearings, and gears, and its structure is complex. When the transmission system is working, the meshing force of the gear pair is transmitted to the shaft and bearing, causing the system to deform, thereby shifting the relative installation position of the gears. The offset of the installation position of the gear pair under load is defined as the meshing misalignment of the gear pair.
Where O, Q, A, B are the points before and after deformation, R_OA, R_OB, R_OQ are the vectors from the origin O to points A, B, and Q, respectively, ΔΣ is the relative change in the axis intersection angle, and ΔP, ΔW, ΔE are the relative displacements along the pinion axial direction, gear axial direction, and offset direction, respectively.
2.2 Calculation Method of Meshing Misalignment
Where P, G, P’, G’ are the projection points of the midpoints of the tooth width of the small and large gears on the gear axis before and after deformation, δP, δW are the distances from point P’ to G and G’, respectively, s1, s2 are the direction vectors of the tangents at points P’ and G’, respectively, n is the normal vector of s1 and s2, θS is the angle between s1 and s2, and lE is the distance between vectors s3 and n.
The equations for calculating the meshing misalignment are as follows:
DeltaP=lP2−∣∣RQP∣∣
DeltaW=lW2−∣ROG∣
DeltaE=lE−∣∣ROQ∣∣
DeltaΣ=θS−θ1
Where l_P2, l_W2, l_E are the distances calculated based on the geometric relationships in Figure 2, R_{QP}, R_{OG}, R_{OQ} are the vectors from point Q to points P, G, and O, respectively, and θ1 is the initial axis intersection angle.
3. Comparison of Transmission Shaft Deformation Analysis with Different Calculation Models
The deformation of the transmission shaft under load is the main factor affecting the meshing misalignment of the gear pair. Therefore, accurately calculating the deformation of the transmission shaft is crucial. The transmission shaft is mostly simplified to a beam element model, and its deformation analysis principle.
The total stiffness matrix of the entire transmission shaft is obtained by superimposing the stiffness matrices of each beam element:
K1n=K12+K23+…+K(n−2)(n−1)+K(n−1)n
The force balance equation of the beam is constructed as follows:
[F1,F2,…,FT=K1n⋅[δ1,δ2,…,\T
To compare the error of the shaft deformation analysis with different models, a complex transmission shaft is taken as an example. The beam element model and solid finite element model of the shaft are established, and the material, force conditions, and boundary conditions of the two models are set the same. The deformation of the transmission shaft obtained through statics analysis.
To compare the deformation of the transmission shaft of the two models intuitively, the deformation of the nodes on the shaft axis is extracted, as shown in Table 1.
| Node Number | Element Type | X_b (μm) | Y_b (μm) | Z_b (μm) |
|---|---|---|---|---|
| 5 | Beam | 1.596 | 1.428 | 3.804 |
| FEA | 1.765 | 1.543 | 4.983 | |
| 6 | Beam | 1.593 | 1.417 | 3.804 |
| FEA | 1.784 | 1.548 | 4.983 | |
| 7 | Beam | 1.590 | 1.406 | 3.804 |
| FEA | 1.785 | 1.540 | 4.983 | |
| 8 | Beam | 1.544 | 1.365 | 3.804 |
| FEA | 1.767 | 1.519 | 4.983 | |
| 9 | Beam | 1.497 | 1.323 | 3.804 |
| FEA | 1.748 | 1.496 | 4.983 |
As can be seen from Table 1, the deformation of the transmission shaft calculated using the beam element model has errors of about 13%-16% in the radial direction and about 30% along the axis direction compared with the solid finite element model. Therefore, when the transmission shaft structure is complex, the beam element model cannot be used to replace the solid finite element model for analyzing its deformation under load. This error may stem from the assumptions of the relationship between the beam cross-section and axis after deformation in the beam element model.
4. Step-by-Step Meshing Misalignment Analysis Model
4.1 Transmission Shaft Coupling Analysis Model
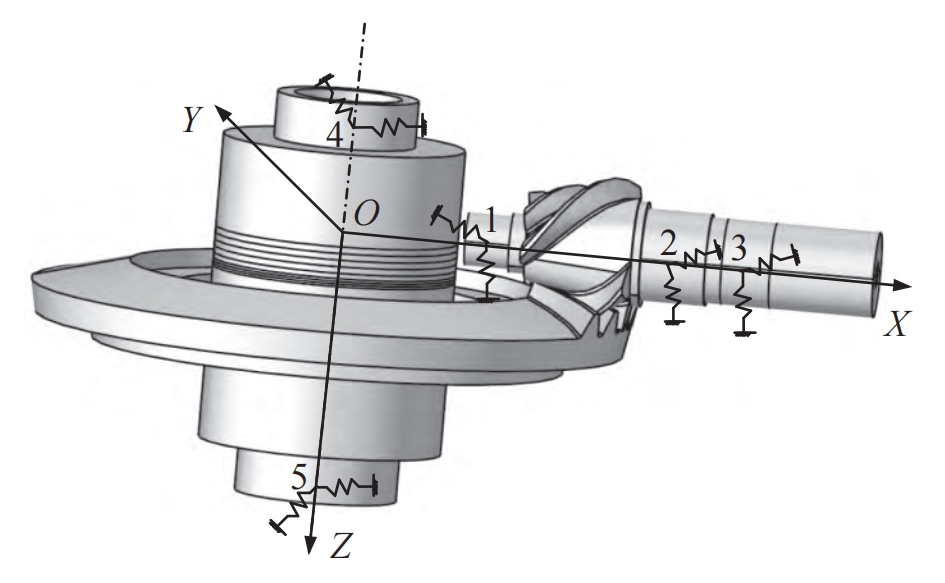
First, a coupling analysis model of transmission shaft deformation considering the influence of bearings is established, as shown in Figure 6. The transmission shaft is divided into segments according to different shaft sections, and all are meshed with hexahedral elements to reduce the number of elements. The mesh is then adjusted based on the bearing installation position, meshing force application position, and deformation extraction position.
Guide points are established at the equivalent force points of the bearings on these shaft segments, and the bearings are coupled with the upper surface grid of the corresponding shaft segment. Considering the elastic characteristics of the bearings, they can be equivalent to springs. Each guide point constrains its five degrees of freedom except for the rotation direction through five springs. The stiffness of each spring in each direction is determined by the value on the main diagonal of the bearing stiffness matrix.
Segments 6 and 7 are the installation positions of the large and small gears. The meshing force of the gear pair needs to be applied at these segments, and the deformation of the transmission shaft under load needs to be extracted. Usually, the node position at the middle of the tooth width is defined as the center position of the contact area. When applying the meshing force to the transmission shaft, an axial section is cut out at point P in the middle of the tooth width (the position of point P is shown in Figure 6), a guide point is established at the shaft center and coupled with the section, and the meshing force and bending moment are applied to this guide point. In addition, the shaft segment is equally divided into several sub-segments, and several guide points are established at the shaft center position in sequence from left to right and coupled with the corresponding axial sections. Through the above processing, the deformation of the gear at the installation position can be represented by the displacement of each guide point.
4.2 Calculation of Equivalent Meshing Force
To reduce the calculation amount of tooth surface contact analysis, the gear contact action is equivalent to a meshing force [9]. The tangential force at the node is calculated based on the transmission torque, and the axial force and radial force are further calculated considering the parameters of the spiral bevel gear. The meshing force calculated above acts on the tooth surface, while the calculation model described in Section 3.1 applies the meshing force to the axis. After changing the point of force application, the load needs to be recalculated using the force translation theorem. Among them, the radial force does not produce a bending moment when translated towards the shaft center, the tangential force produces a bending moment around the axis rotation direction which does not affect the deformation, and the axial force produces bending moments in other directions that affect the deformation.
The bending moment produced by the axial force of the pinion in the zP direction is:
MZP=FaxlW1
When the offset distance of the gear pair is 0, the bending moment calculation method of the gear is the same as that of the pinion. However, when the offset distance is not 0, the direction of the bending moment produced by the axial force of the gear has a certain angle with the z direction, so the bending moment coordinate system at the guide point of the gear shaft center is different from the meshing force coordinate system. To avoid the problem of adding two different coordinate systems when applying meshing force and bending moment at the same guide point, the bending moment coordinate system is taken as the main system, and the tangential force and radial force are decomposed into this coordinate system. The calculation formulas are as follows:
FX′=Fmtsinθ+Frdcosθ
FZ′=Fmtcosθ+Frdsinθ
MZ′=FaxlP2+lW12
The meshing force and bending moment are applied at the guide points of the axial section at the middle of the tooth width in the pinion coordinate system and gear coordinate system, respectively.
4.3 Loaded Contact Analysis of Gear Teeth Considering Meshing Misalignment
The equivalent meshing force calculated in Section 3.2 is substituted into the transmission shaft deformation coupling analysis model described in Section 3.1, and the displacement deformation of multiple guide points on the transmission shaft axis in the model is exported. This is then substituted into the formula in Section 2.2 to obtain the meshing misalignment of the system. By adjusting the position and attitude of the gears in the multi-tooth meshing model based on the meshing misalignment [10], the loaded contact analysis model of the gear teeth considering the meshing misalignment is constructed.
The tooth surfaces of the gears establish a meshing action through contact pairs. A reference point for load application is established at the center of the axis in the middle of the tooth width of the large and small gears, which is coupled with the hub surface of the gears to apply the load. The working torque is applied to the reference point of the large gear, and the rotation angle is applied to the reference point of the pinion, while the other degrees of freedom except for the gear rotation freedom are constrained. The contact state of the tooth surface at a certain meshing instant and the actual rotation angle of the gear can be obtained by static analysis. By changing the rotation angle of the pinion for multi-step calculations, the loaded transmission error and contact pattern of the gear pair during the entire meshing process can be obtained.
5. Calculation Example
5.1 Comparison of Meshing Misalignment Calculation
To verify the accuracy of the step-by-step meshing misalignment analysis method for spiral bevel gear transmission systems based on the solid finite element method proposed in this paper, the meshing misalignment of the gear pair is analyzed using the drive axle of a passenger car as an example. The basic parameters of the spiral bevel gear is shown in Table 2.
| Basic Parameter | Pinion | Gear |
|---|---|---|
| Number of teeth | 7 | 43 |
| Modulus (mm) | 10.512 | |
| Axis intersection angle (°) | 90 | |
| Offset distance (mm) | 46 | |
| Pressure angle (°) | 22.5 | |
| Tooth width (mm) | 81.6 | 174.00 |
| External cone distance (mm) | 238.77 | 230.58 |
| Helix angle (°) | 48.083 | 334.345 |
| Pitch cone angle (°) | 11.100 | 78.583 |
The rated working torque of the gear pair is 15,000 N·m. The meshing force and bending moment calculation results obtained using the calculation formula described in Section 3.2 are shown in Table 3.
