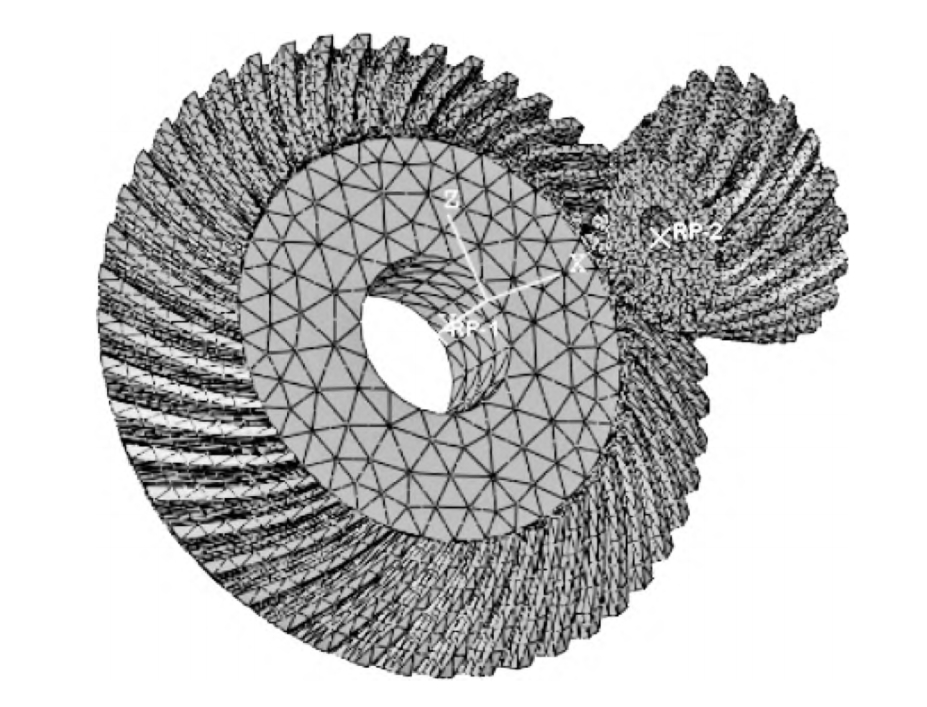
Bevel gears, especially spiral bevel gears, are widely used in various mechanical transmissions due to their excellent performance in power transmission. However, the complex structure and numerous parameters of spiral bevel gears make their modeling a challenging task. In this article, we will explore the parametric precision modeling of bevel gears using MATLAB and Creo Parametric, and discuss the application of 3D printing technology in validating the effectiveness of the parameterized models.
Introduction
Spiral bevel gears have more meshing teeth and better load-carrying capacity compared to straight bevel gears with the same number of teeth and modulus. However, the complexity of their parameters and structure makes modeling more difficult. Many scholars have conducted extensive research on the establishment of spiral bevel gear models, but most literature lacks detailed descriptions of the specific modeling steps, resulting in weak operability.
Calculation and Derivation of Bevel Gear Parameters
In the MATLAB software, a real-time script file is created to define the basic parameters of the bevel gear, such as the pressure angle, number of meshing teeth, modulus, top clearance coefficient, number of teeth, tooth width, addendum height coefficient, and displacement coefficient. Through the operation relationships between these variables, the calculation parameters of the bevel gear can be derived. For example, the diameters of various circles at the large and small ends, as well as the lengths of various generatrices, can be calculated. The root cone angle is determined based on certain conditions to ensure the gear’s performance.
| Code | Name | Parameter Calculation Value |
|---|---|---|
| d/mm | Pitch Circle Diameter | 100 |
| h/mm | Addendum Height | |
| 8/(°) | Cone Angle | 29.0546 |
| Rx/mm | Pitch Cone Distance | 102.9563 |
| R/mm | Cutter Radius | 85.7969 |
| () | Tooth Top Angle | 2.2249 |
| b/mm | Tooth Top Width | 32.0241 |
| d/mm | Tooth Top Circle Diameter | 106.9933 |
| h/mm | Dedendum Height | 5 |
| 0() | Tooth Root Angle | 2.7803 |
| b/mm | Tooth Root Width | 32.0377 |
| d/mm | Tooth Root Circle Diameter | 91.2584 |
| d/mm | Base Circle Diameter | 93.9693 |
| h /mm | Base Height | 3.4495 |
| (°) | Base Angle | 1.9189 |
| b/mm | Base Width | 32.0180 |
| h/mm | Whole Tooth Height | 9 |
| 8() | Top Cone Angle | 31.2795 |
| 8/() | Root Cone Angle | 27.1357 |
| 8() | Base Cone Angle | 27.1357 |
| d/mm | Large End Tooth Root Circle Diameter | 104.3959 |
| d/mm | Large End Base Circle Diameter | 107.4970 |
| d/mm | Large End Pitch Circle Diameter | 114.3959 |
| d/mm | Large End Tooth Top Circle Diameter | 122.3959 |
| d/mm | Small End Tooth Root Circle Diameter | 71.9484 |
| d/mm | Small End Base Circle Diameter | 74.0857 |
| d /mm | Small End Pitch Circle Diameter | 78.8403 |
| d/mm | Small End Tooth Top Circle Diameter | 84.3538 |
| d/mm | Top Cone Generatrix Length | 53.4966 |
| d /mm | Pitch Cone Generatrix Length | 50 |
| d /mm | Base Cone Generatrix Length | 46.9846 |
| d /mm | Root Cone Generatrix Length | 45.6292 |
Modeling of Bevel Gear Blanks
- Parameter Definition
In the Creo Parametric 9.0 software, the parameter names and basic parameter values used in the modeling process are defined in the dialog box. The parameter values that need to be calculated are initially set to 0 and edited one by one. Then, in the “d = Relationship” dialog box, the basic relationship calculation formulas for the bevel gear are entered. - Drawing of Bevel Gear Involute
A new reference plane DTM1 is created on the TOP surface, and an axis A_1 is created by selecting the RIGHT and FRONT surfaces simultaneously. A point PNT0 is created by selecting DTM1 and A_1. On the RIGHT surface, the basic geometric relationships are sketched, including the pitch cone distance, tooth width, and angles between the back cone generatrices and the pitch cone generatrix. The four circles at the large end, namely the tooth top circle, pitch circle, base circle, and tooth root circle, are drawn on the reference plane DTM2 based on the large back cone generatrix and axis. Similarly, the four circles at the small end are drawn.
The large end involute is drawn by connecting a point on the tooth root circle to the center and creating a coordinate system CS0. The coordinate system CS1 is created by rotating CS0 around the Z-axis. Using the “d = Relationship” command, the relationship “D27=360COS(DELTA)/(4z)+180*TAN(ALPHA)/PI-ALPHA” is added, and the large end involute expression is set. The small end involute is created similarly.
A “mixed scan” command is used to select the tooth top circle, tooth root circle, and two involutes at the large end for projection and trimming. A complete straight tooth is obtained, and by copying, pasting, and rotating this tooth, the parameterized straight bevel gear is completed.
Modeling of Straight Bevel Gears
To model a straight bevel gear, the involute curve group is drawn. Using the curve command through points, the curve is drawn, and the redundant involutes at the large and small ends are trimmed. The involutes at the large and small ends are connected to the centers of the corresponding ends. The rotation reference angles for the curve groups at the small and large ends are sketched on the small and large circular surfaces of the gear blank, respectively.
| Step | Description | Image |
|---|---|---|
| 1 | Draw the basic geometric relationships on the RIGHT surface, including the pitch cone distance, tooth width, and angles between the back cone generatrices and the pitch cone generatrix. | [Image 1] |
| 2 | Draw the four circles at the large end on the reference plane DTM2 based on the large back cone generatrix and axis. | [Image 2] |
| 3 | Create the large end involute by connecting a point on the tooth root circle to the center and defining the coordinate system. | [Image 3] |
| 4 | Draw the small end involute similarly to the large end. | [Image 4] |
| 5 | Use the “mixed scan” command to project and trim the components at the large end to form a complete straight tooth. | [Image 5] |
| 6 | Copy, paste, and rotate the tooth to obtain the complete parameterized straight bevel gear. | [Image 6] |
[Insert relevant images for each step]
Modeling of Spiral Bevel Gears
- Moving the Involute Curve Groups
The involute curve groups at the large and small ends are moved separately. For the large end, after selecting the trimmed curve group and using the “Copy – Paste (Selective Paste)” command, in the “Move (Copy)” dialog box, the type is selected as rotation, the reference is the central axis of the gear blank, and the “offset” is filled with the referenced rotation angle at the large end. The same process is applied to the small end involute curve group. - Scanning and Mixing the Surface Patches
A “scan mix” is used to connect the surfaces of the involute curve groups at the large and small ends. First, one side of the large end involute curve group and one side of the small end involute curve group are connected, and then the same process is repeated for the other sides. The two surfaces are merged into one. - Boundary Mixing and Fusion with the Gear Blank
The curves at the large and small ends are stitched using the “boundary mix” command. First, the curves at the small end are stitched, and then the curves at the large end are stitched in the same way. The two scanned and mixed surface patches are then boundary mixed, and a merged quasi-tooth surface skin is obtained.
The surface group and the gear blank entity are “fused” together. A straight line is drawn based on the generatrix of the root cone, and a surface is rotated around the rotation center of the gear blank. The rotated surface and the surface group are merged.
- Creating the 准齿面 and Making It Solid
The first quasi-tooth surface is obtained by merging the above steps into a group in the project tree and performing a “mirror” operation on this group. The purpose is to convert the tooth surface to left-hand rotation. The first quasi-tooth surface is hidden, and the mirrored quasi-tooth surface is retained. It is then “copied – pasted (selective paste) – applied move/rotation transformation to the copy”. In the “Copy (Move)” dialog box, the “axis” is selected, and the axis of the gear blank is clicked. The rotation angle is calculated to be 14.4°. The copied quasi-tooth surface is “arrayed”, with the first direction selected as the axis of the gear blank and the number of members selected as Z – 1.
Since the quasi-tooth surface is only a surface patch and not a solid, it needs to be solidified. The mirrored quasi-tooth surface group is selected, and the “solidify” command is used. In the pop-up dialog box, the type is selected as “fill solid”. At this point, the mirrored quasi-tooth surface group becomes a solid model. The same solidification operation is performed on the adjacent second quasi-tooth surface group, and after the second solidification result is arrayed, the entire 25 quasi-tooth surface groups become solids.
- Removing Unnecessary Parts and Creating the Final Model
The parts outside the yellow tooth top cone surface patch in the production application of the spiral bevel gear need to be removed. A surface is drawn based on the generatrix of the top cone, and the “remove material” command is used. Finally, a through hole with a diameter of 30 mm is drawn in the middle of the spiral bevel gear model to obtain the final spiral bevel gear entity model.
| Step | Description | Image |
|---|---|---|
| 1 | Move the involute curve groups at the large and small ends separately. | [Image 7] |
| 2 | Scan and mix the surface patches of the involute curve groups. | [Image 8] |
| 3 | Perform boundary mixing and fusion with the gear blank. | [Image 9] |
| 4 | Create the first quasi-tooth surface and mirror it. | [Image 10] |
| 5 | Solidify the quasi-tooth surfaces and array them. | [Image 11] |
| 6 | Remove unnecessary parts and create the final model. | [Image 12] |
[Insert relevant images for each step]
3D Printing of Bevel Gears
The parameterized modeled bevel gears are exported in STL format from Creo Parametric 9.0 and sliced in the slicing software. The key parameters for 3D printing are set as follows: layer height 0.2 mm – 1.2 mm; bottom and top layer thickness 1.0 mm, fill density 10%; print speed 40 mm/s, nozzle temperature 210°C, hot bed temperature 40°C; support type is local support, platform attachment type is bottom edge; print material is PLA, diameter 1.75 mm, extrusion amount is 100%; machine nozzle diameter 0.4 mm, retraction speed of filament 40 mm/s, retraction length 4 mm; initial layer thickness 0.2 mm, initial layer line 100%, bottom layer is not cut, two extrusion overlaps 0.15 mm; movement speed, bottom layer print speed, fill print speed, top and bottom print speed, outer wall print speed, inner wall print speed are all set to 40 mm/s; cooling minimum print time per layer is 5 s, and fan cooling is enabled.
The printed entities of the straight bevel gear and the spiral bevel gear are shown in the figures.
Conclusion
By using the MATLAB software to program and derive the calculation parameters of the bevel gear, the workload of manual calculation is greatly reduced, making the derivation of formulas faster and more accurate. The parametric modeling of straight bevel gears and spiral bevel gears is similar, with the difference lying in the final tooth shape construction. By studying and analyzing the important steps in the bevel gear modeling process, the parametric method is used to model the bevel gear, which greatly reduces the modeling difficulty. Since a new model can be obtained by simply changing the basic parameters, this method is fast, efficient, and accurate, providing a new idea for the modeling of bevel gears. Combined with 3D printing technology, it can obtain the model object more quickly than traditional CNC machine tool processing, saving a lot of manpower and financial resources, which has important practical significance.
In the future, further research can be conducted on improving the accuracy and efficiency of the modeling process, optimizing the design of bevel gears, and exploring more applications of 3D printing technology in the manufacturing of bevel gears. This will contribute to the development of the mechanical transmission industry and the improvement of the performance and reliability of mechanical equipment.