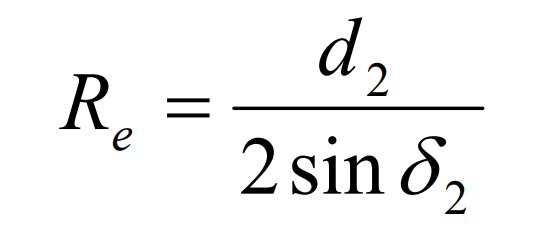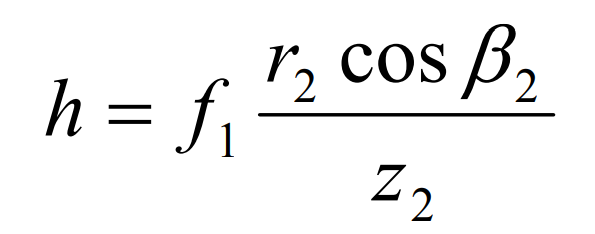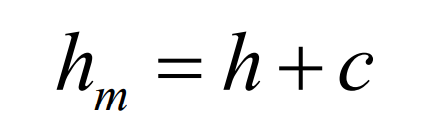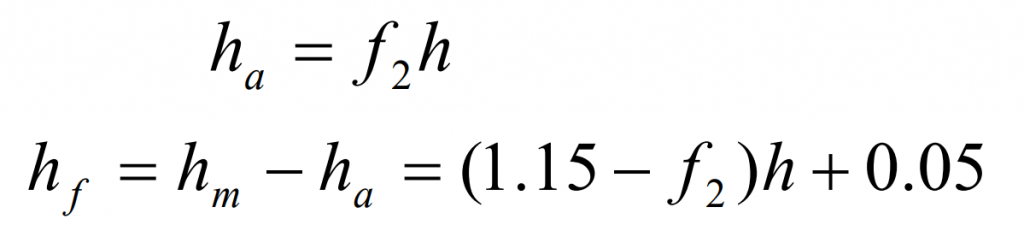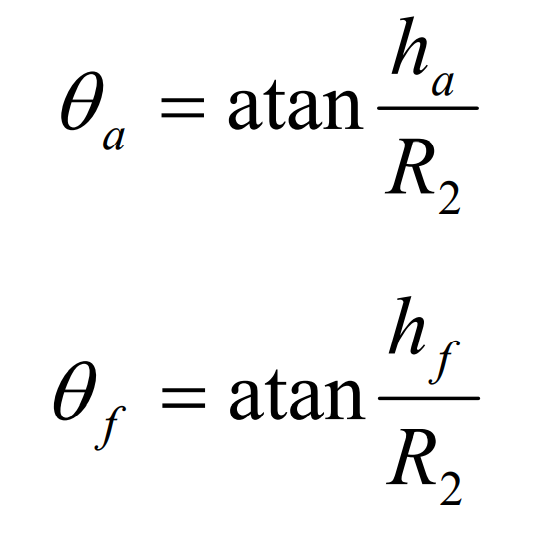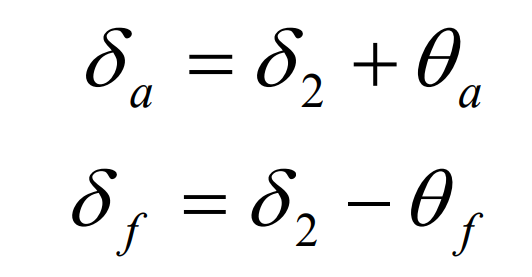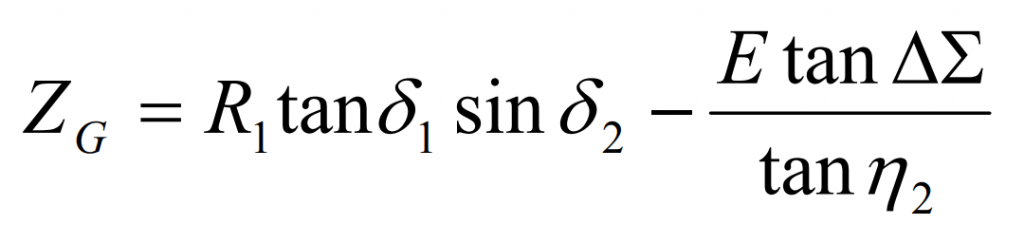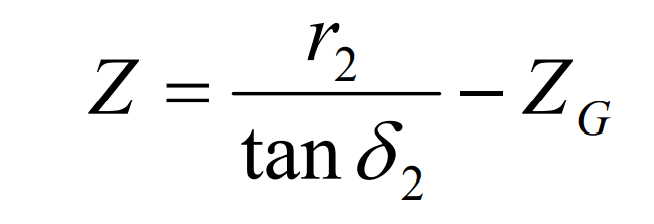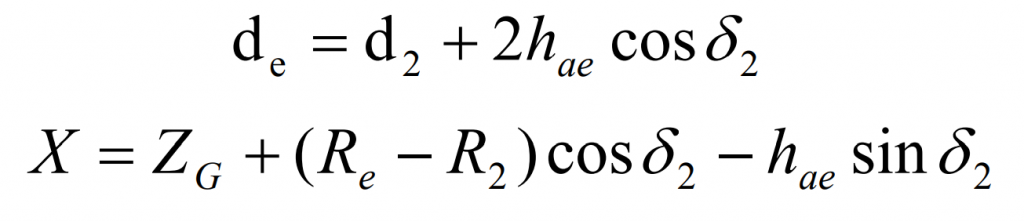The parameters of the large end pitch circle diameter, pitch cone angle, and the distance between the intersection and each vertex of the hypoid gear can be obtained according to these parameters.
According to the geometric characteristics of the large hypoid gear wheel, we can use the following formula to obtain the outer cone distance re of the large hypoid gear wheel:
When determining the tooth top height of hypoid gear, its determination method is different from that of spiral bevel gear. It first calculates the working tooth height at the tooth midpoint of hypoid gear, and then deduces the tooth height of large end and small end according to the calculation formula. The working tooth height h at the midpoint of the large gear of hypoid gear can be calculated by the following formula:
The calculation formula of the full tooth height of the hypoid gear is:
Where, C is the top clearance of hypoid gear, which can be determined by the formula: C = 0.15h + 0.05.
The tooth top height and tooth root height at the midpoint of the large gear of hypoid gear can be obtained by the following formula:
There are three ways to design the tooth root angle of hypoid gear: Standard shrinkage, double shrinkage and root line inclination. In this paper, the tooth root angle of hypoid gear under standard shrinkage is selected. Tooth apex angle of hypoid gear θ A and root angle θ F is calculated as follows:
The tooth apex angle and tooth root angle of hypoid gear can be determined by the above formula. According to the geometric relationship between pitch cone angle and surface cone angle and between pitch cone angle and root cone angle, the surface cone angle and root cone angle of hypoid gear wheel are determined. The calculation formula is as follows:
Therefore, the tooth top height h AE, tooth root height h Fe and full tooth height h t at the outer end of the large gear of hypoid gear can also be determined:
After the basic geometric parameters of the hypoid gear wheel are obtained, the distance from the cone vertex of the hypoid gear wheel root to the intersection point and the distance from the cone vertex of the hypoid gear wheel surface to the intersection point can be calculated. According to the calculated result and the size of zero, the positional relationship between the vertex of face cone and root cone and the intersection can be judged.
The distance ZG between the midpoint along the axis of the hypoid gear wheel and the intersection can be obtained by the following formula:
The distance Z between the vertex of the pitch cone and the intersection can be obtained by the following formula:
Finally, the outer diameter De of the large hypoid gear and the distance x from the crown to the intersection can be determined by the following formula: