The profile of the circular arc curve – Involute – circular arc curve is used, the circular arc curve is used at the top and the bottom of the gear, and the involute curve is used at the side of the gear.Form a set of conjugate curves.
Because of the symmetry of the involute gear profile, we only discuss about 1/14 of the profile.Select the curve PBCQ from the lowest point P of the tooth Valley to the highest point Q of the adjacent tooth peak, which is sandwiched between the angle QOP and QOP=pi/7, as shown in Figure 3.This part of the curve consists of a section of involute BC and two sections of circular arcs PB and CQ, in which the two sections of circular arcs are tangent to the involute at points B and C respectively.
Because of the symmetry of the tooth profile [5], it can be seen that the circular arc is perpendicular to OP and the circular arc CQ is perpendicular to Q.Make tangent (i.e. generating line) of the base circle through B and C respectively, and cut at B’, C’.Since the two arcs are tangent to the involute at points B and C respectively, the point P’at which BB’ intersects with OP is an arc PB.
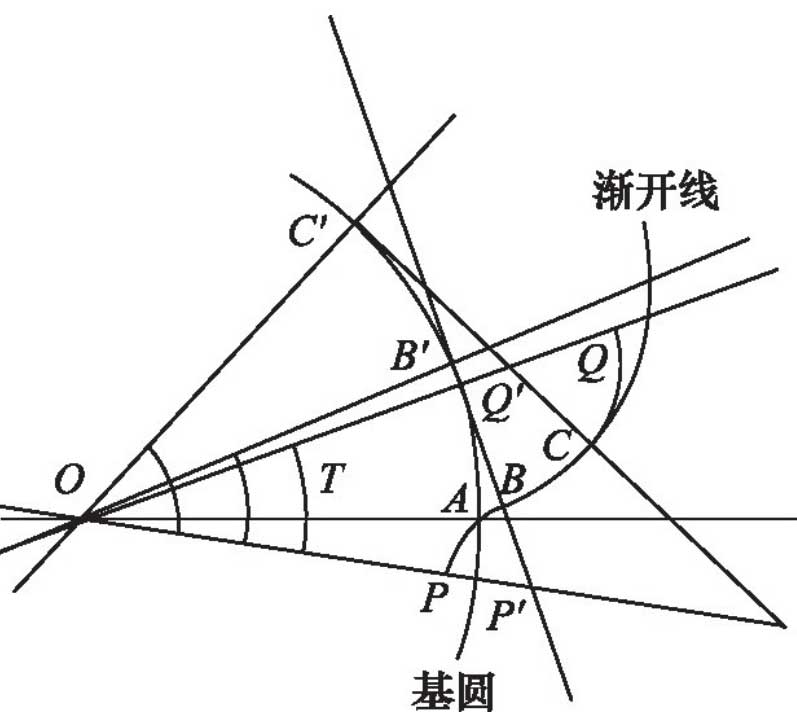
If the radius of the base circle is R and the angles B’OA, C’OA and QOA are a0, X1 and T respectively, the involute part of the tooth profile can be determined by the above four parameters.The four parameters are used to calculate the involute equation, the coordinates and radii of P’, C’, BP’, CQ’, so as to determine the expressions of large circle radius_=OQ and small circle radius=OP.
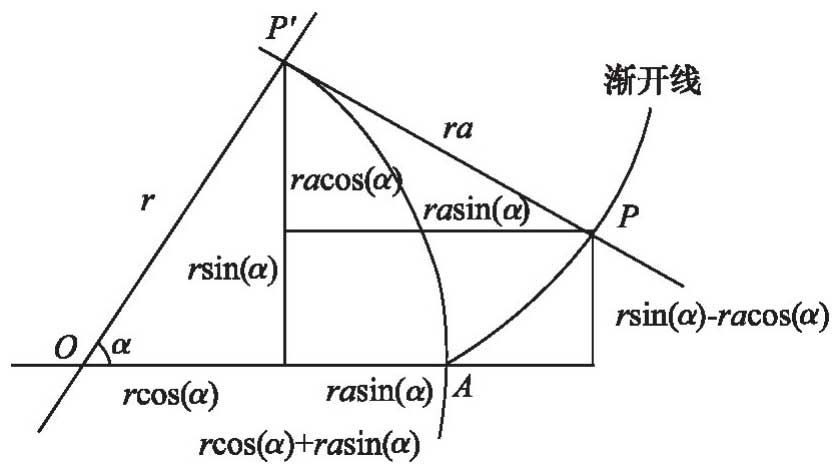
Set the line from the center of circle O to the base point A as the x-axis positive direction and the O-point as the coordinate origin to establish the right-hand system plane coordinate system.For any point P on the involute, the tangent of the base circle through the point P is the involute generating line. Set the tangent point P’, and the angle POA a.
