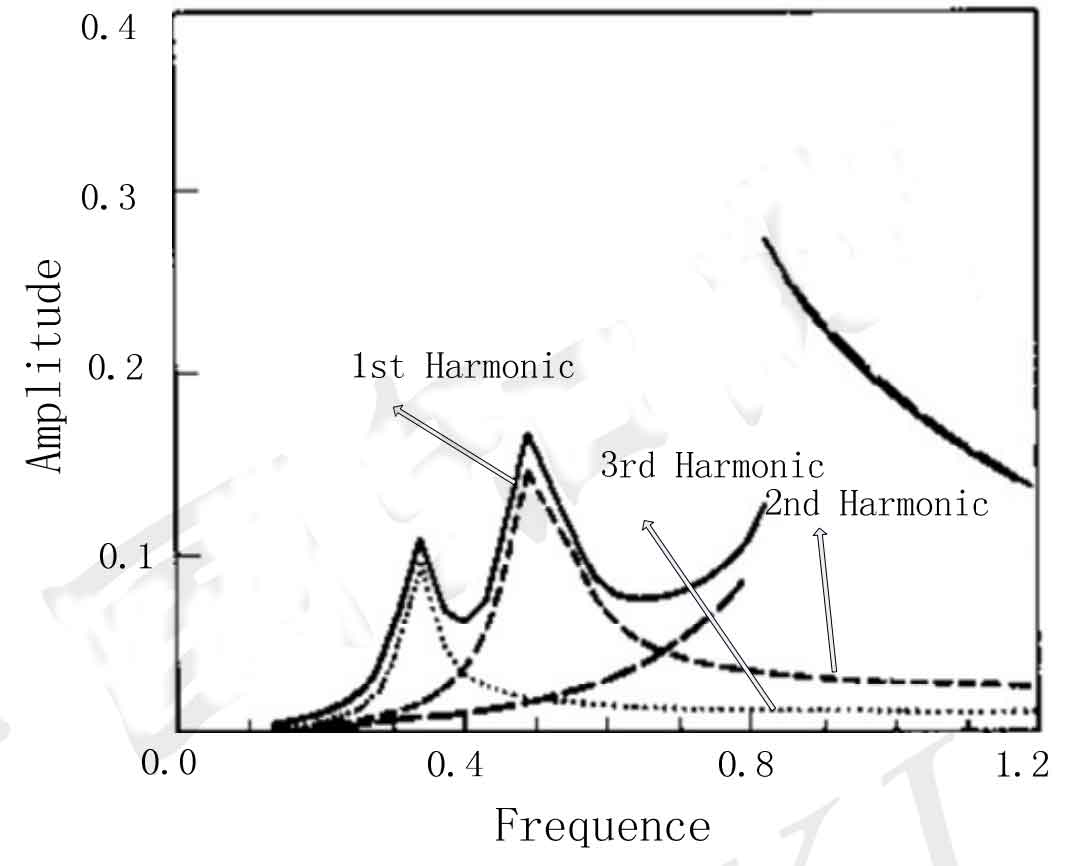
The dynamic excitation of spur gear transmission system is an important part of studying the dynamic characteristics of spur gears, and it is also the main source of vibration and noise of spur gears. For the loading mode of spur gear dynamic excitation, many scholars at home and abroad have done a lot of research from different angles using different solutions. A. Kahraman et al. Studied the nonlinear dynamic characteristics caused by the backlash in the spur gear and the internal excitation caused by the transmission error. On this basis, they analyzed the influence of the internal excitation and external excitation on the dynamic characteristics of the spur gear. The figure is the third-order harmonic frequency response curve of the transmission system under the given load and damping.
T. Tsuta et al. Wrote the dynamic excitation force of spur gear as the product of spur gear meshing stiffness and spur gear error, and gave the mathematical expression of spur gear meshing impact on this basis. Chengaiming et al. Used the finite element method to analyze the meshing stiffness of the internal translational spur gear pair, and obtained that the meshing comprehensive stiffness of the internal translational spur gear pair has the excitation of multi-order harmonic components that can not be ignored. Considering the time-varying meshing stiffness of multi tooth contact and tooth side clearance and other nonlinear factors, the dynamic equation of the internal translational spur gear system is derived, The phase diagram and Poincare map in the case of excitation frequency and damping ratio are given by numerical calculation. The results show that the number of cycles and the impact vibration characteristics of the system have complex changes with the excitation frequency and damping ratio. The inherent law of nonlinear vibration of spur gear transmission system in virtual simulation environment is revealed, and the nonlinear system model of spur gear bearing shaft coupling is established. Considering the internal and external excitation of the transmission system, the dynamic characteristics of the transmission system are simulated. The power spectral density, time history curve and phase trajectory are analyzed. The numerical results of nonlinear dynamics are basically consistent with the finite element calculation results, which shows that the combination of the two methods can accurately predict the dynamic response of the system and the internal law of vibration signals, and provide a theoretical basis for the dynamic design of the system.
Lim et al. Constructed the lumped parameter model and simplified the spur gear dynamic equation by using the elastic finite element method. Parke et al. Analyzed the internal excitation such as stiffness excitation and error excitation in the process of spur gear meshing, and analyzed the dynamic response of spur gear pair at different speeds and torques by using the finite element method. Lirunfang, lintengjiao, etc. transformed the nonlinear dynamic differential equation of internal excitation and time-varying meshing stiffness into an approximate linear dynamic differential equation, and used the three-dimensional finite element method to calculate the time-varying meshing stiffness and the three-dimensional contact finite element method to solve the impact excitation force, while the error excitation was calculated using the gear tooth deviation specified in the accuracy grade, Finally, the dynamic excitation force is applied to the whole finite element model to obtain the dynamic vibration response.
P. Velex et al. Gave the contour of dynamic excitation in Fourier form, and gave the influence law of spur gear geometric parameters on dynamic excitation. 50. Vedmar uses the deformation of spur gear and bearing to finally determine the meshing stiffness and contact mode, analyzes the dynamic influence of friction on spur gear contact, provides a new method for calculating the dynamic load of spur gear, and considers the time-varying meshing stiffness, tooth friction and bearing stiffness of spur gear, and analyzes the dynamic load of spur gear transmission system under different working conditions. After taking into account the flapping vibration of spur gear teeth under the impact of forward and reverse meshing, wangyuxin et al. Gave the calculation expression of dynamic load under the excitation of static transmission error, time-varying meshing stiffness, spur gear tooth side clearance, and spur gear friction torque. Vaishya and Singh build a spur gear dynamic model by using periodic meshing stiffness and assuming that the load is evenly distributed between the teeth and the dynamic transmission error, and use Floquet theory and harmonic balance method to solve the dynamic equation. The simplification of load distribution is conducive to the solution of the equation, but it can not truly reflect the actual situation of spur gear.
