In the early research, because the dynamic impact theoretical analysis and experimental analysis of tooth friction are also limited, the tooth friction is often ignored. However, the research shows that the spur gear vibration and noise are still very large even if the transmission error of spur gear is unilaterally reduced because the spur gear tooth surface friction has an exciting effect on the bearing dynamic support force. Figure 1 shows the adopted tooth surface friction torsion model. The model in the figure considers the tooth surface friction in the normal direction of the meshing line to build the spur gear dynamic equation:
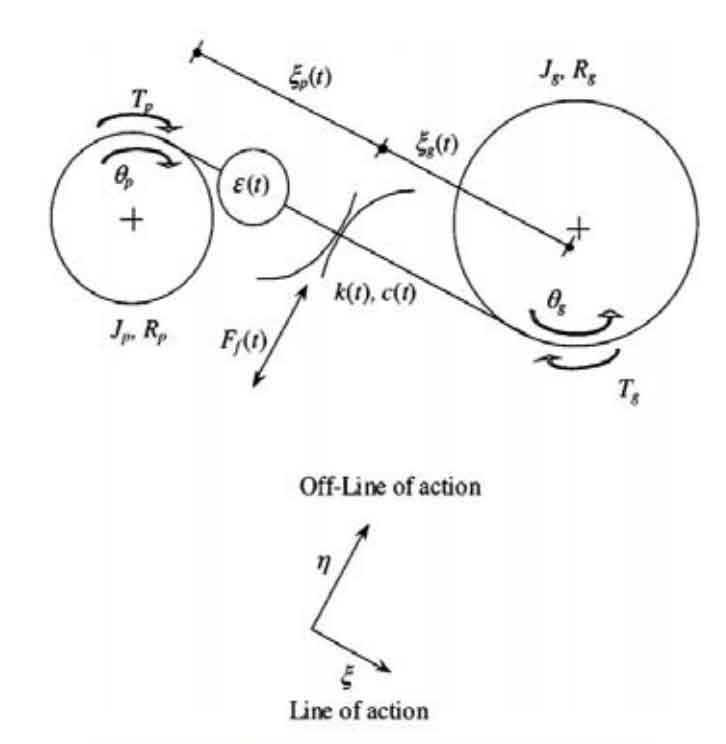
Coulomb friction is more used in the established dynamic model, and quasi-static methods are used to calculate the normal force, load distribution rate and sliding speed to study the influence of tooth friction on the excitation system. After summarizing and reviewing the early literatures, vaishya and Singh assumed that the load between spur gears was evenly distributed, constructed the dynamic equation containing tooth surface friction with rectangular square wave stiffness, and solved the dynamic equation of single degree of freedom spur gears by using Floquet theory and harmonic balance method. Figure 2 shows the meshing stiffness of spur gears in the form of rectangular waves:
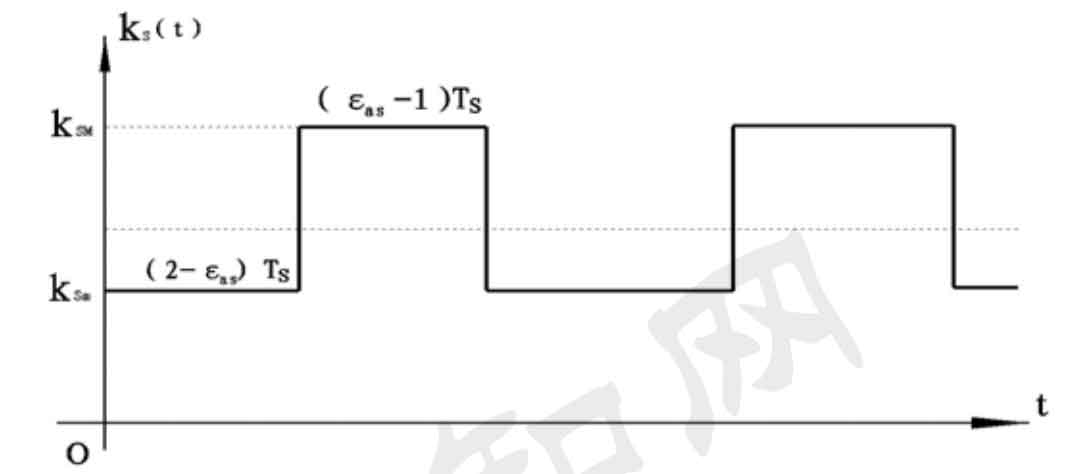
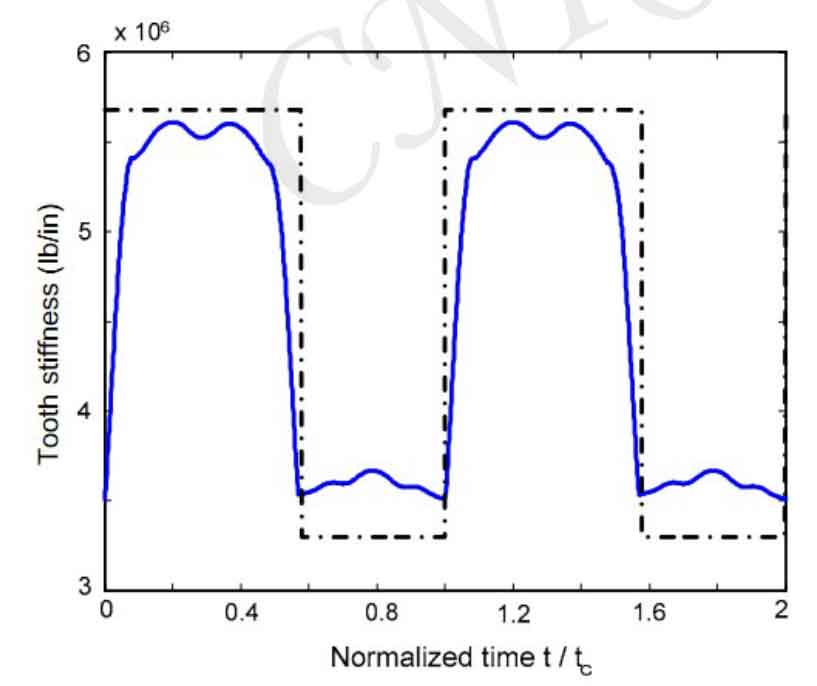
The assumption of average load distribution simplifies the expression of the equation and reduces the difficulty of solution, but this simplification is far from the actual meshing situation. Figure 3 shows the tooth stiffness curve under average load and actual load.
Lundvall et al. Considered the tooth profile modification and manufacturing error in the multi degree of freedom spur gear dynamic model, used the numerical method to solve the influence of tooth surface friction on dynamic characteristics, and studied the influence of tooth profile modification on transmission error when considering tooth surface friction. After experimental analysis, Houser et al. Learned that friction has an important impact on load transmission when it deviates from the direction of the meshing line, and this effect becomes particularly obvious under the condition of high torque and low speed. Velex and cahouet used recurrence program to analyze the influence of tooth surface friction on dynamic characteristics, and analyzed the support force in helical gear system under the condition of considering tooth deviation and time-varying meshing stiffness. The results showed that there was an oscillation force under low speed conditions. After analysis, these oscillation forces were caused by the friction between teeth. As shown in Figure 4, the influence curve of helical gear tooth surface friction on the support force of transmission system. In the following research, velex and sainsot[61] found that the tooth surface friction is a non negligible excitation source for spur and helical gears without errors, especially for the translational vibration in spur gears with large coincidence.
However, it is difficult to solve the dynamic equation when the nonlinear factors such as time-varying friction and time-varying meshing stiffness are taken into account in the multi degree of freedom spur gear system. In the above mentioned model, the tooth surface friction mostly adopts Coulomb friction, and the friction coefficient adopts a constant value. This is mainly because it is difficult to measure the tooth surface friction. In practice, the thickness of the lubricating oil film changes with the rotation of the spur gear, which changes the meshing attribute and leads to the instantaneous change of the friction. Therefore, the friction coefficient changes instantaneously with the meshing position of the gear teeth and the direction of friction near the nodes. Fig. 5 shows the change of friction coefficient along the spur gear tooth profile. The friction coefficient at the tooth root is the smallest and the friction coefficient at the tooth top is the largest.
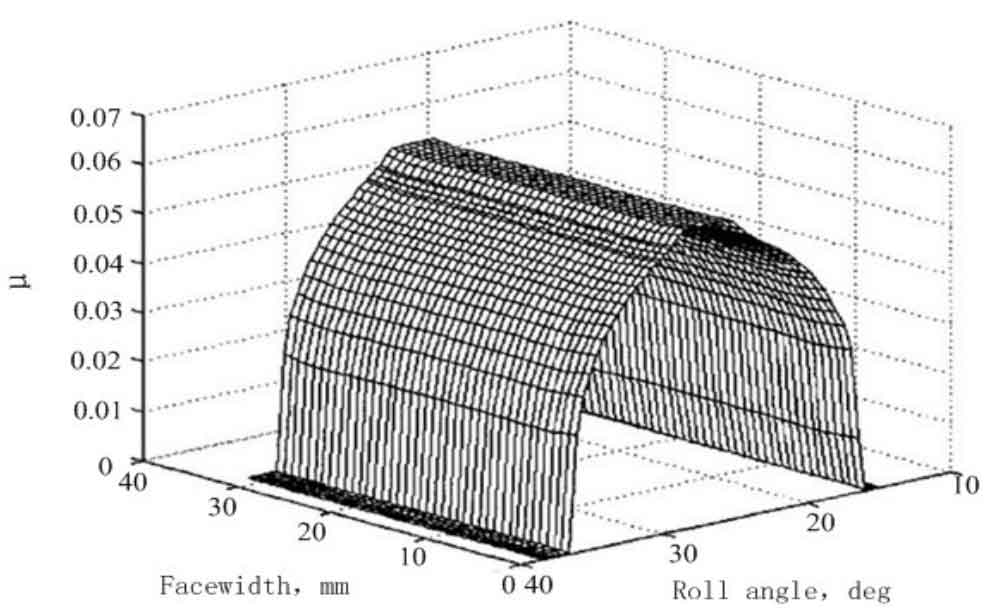
Valentin et al. Carried out experimental research through the dynamic detection device. The research results show that the tooth friction is also one of the sources of vibration and noise. In the spur gear box system, most of the methods such as finite element, boundary element and theoretical analysis are used to calculate the tooth friction. The experimental results show that the friction load has an important impact on the deviation of the meshing line when it is transmitted between the bearing and the spur gear box, Especially in the condition of high torque and low speed, this effect is more obvious. Duan and Singh put forward a smooth Coulomb model for dry friction, which can make the spur gear have a smooth motion at the nodes. Hamrock and Dawson used the experimental method to predict the minimum oil film thickness between two disks in linear contact, and calculated the oil film parameters to obtain the mixed lubricating oil film, so as to calculate the tooth surface friction coefficient. Rebbechi et al. Successfully calculated the tooth surface friction by using the change law of tooth root stress. Vaishya and user[71] have shown that it is possible to calculate the friction under quasi-static conditions by using digital filtering technology. At present, alternative friction theories, such as elastohydrodynamic lubrication, boundary lubrication and hybrid lubrication, have been adopted to explain the tooth surface friction under different conditions.
