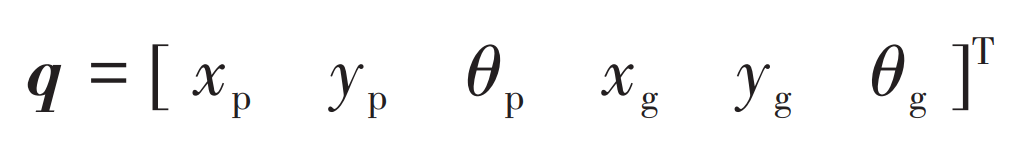As shown in Figure 1, the 3-DOF bending torsion coupling dynamic model of spur gear pair is established by using the mass concentration method. The displacement of spur gear in the X direction is Xi (I = P, g), the displacement in the Y direction is Yi (I = P, g), and the displacement in the rotation direction around the spur gear shaft is θ I (I = P, g), X direction, Y direction and θ The direction is shown in Figure 1. The subscript p is the driving wheel and G is the driven wheel.
The displacement vector of mass point is:
Considering the tooth surface friction, time-varying meshing stiffness and random error, the corresponding bending torsional vibration equation shown in Figure 1 is:
Where, KXI is the equivalent support stiffness of the main driven gear in the X direction; Kyi is the equivalent support stiffness of the main driven gear in Y direction; Km (T) is the time-varying meshing stiffness of the spur gear; Ti (T) torque of main driven gear; RI (T) meshing curvature radius of the main driven gear along the contact line; Mi the mass of the main driven gear; II is moment of inertia; F (T) is the time-varying friction force under the random roughness of spur gear teeth; α Is the pressure angle of the spur gear pair; E (T) is the spur gear error.
| Parameter | Driving wheel | Driven wheel |
| Number of teeth | 33 | 26 |
| Accuracy class | 6GJ | 6GJ |
| Mass / kg | 10.6 | 7.43 |
| Modulus / mm | 7 | 7 |
| Moment of inertia (/ kg ⋅ mm2) | 147 670 | 61 426 |
| Pressure angle (/ °) | 20 | 20 |
| Tooth width / mm | 69 | 69 |
| Input speed (/ R / min) | 2 000 | 2 000 |
| Input torque (/ N ⋅ m) | 2 340.7 | 2 340.7 |
The spur gear pair for a transmission is taken as the research object, and its parameters are shown in the table.
The time-varying meshing stiffness curve is calculated according to the numerical integration formula of Weber energy method, as shown in Figure 2.