In order to obtain the dynamic engagement stiffness in the process of gear transmission, besides determining the engagement positions, the dynamic boundary conditions of the single and double teeth engagement and the modification area need to be determined.When calculating meshing stiffness by quasi-static method, the boundary conditions of single and double teeth engagement and modification area remain unchanged due to fixed constraints imposed on the center position of each gear.
In actual gear transmission, the boundary conditions of single and double teeth engagement and modification area of gears change with the change of center distance.The meshing boundary conditions of single and double teeth are shown in the figure. In the figure, alpha A is the pressure angle of the top circle of the gear 1 and alpha D is the pressure angle of the meshing point of the gear when the gear 1 exits the meshing, which can be obtained from the geometric analysis:
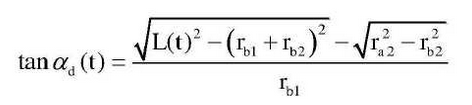
In the formula, gamma B1 and gamma B2 are the base circle radius of gear 1 and gear 2 respectively, gamma A2 is the top circle radius of gear 2 and L(t) is the dynamic center distance.
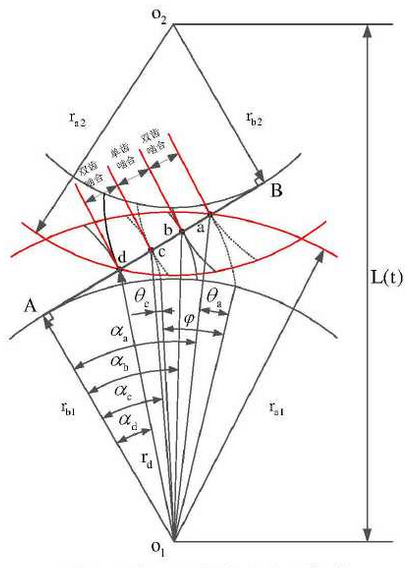
When one of the teeth of gear 1 has just entered engagement, the previous teeth enter the double-tooth engagement area from the single-tooth engagement area, as shown in the figure at point a and point C (the lowest point of single-tooth engagement), the pressure angle of the two points meets:
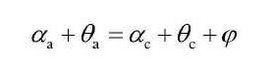
In this formula, Z1 is the number of teeth of gear 1, and theta A and theta C are the involute spread angles of the meshing points a and c, respectively.
