Establish the space right-handed coordinate system, as shown in the figure. The installation center distance of linear gear pair is e, so and SP are fixture coordinate system. S1 and S2 are respectively the coordinate systems which are fixedly connected with the pinion and the ring gear. At the initial moment of meshing, S1 and S2 coincide with so and sp. The pinion and ring gear rotate at angular speed respectively ω 1、 ω 2 moves around the ZO and ZP axes at a constant speed with the same turning direction. After t-step, the rotation angle is θ 1 and θ 2。 In the meshing process, the spatial curves R1 and R2 always keep point contact. The transformation matrix from S1 to S2 can be obtained by coordinate transformation and related parameters
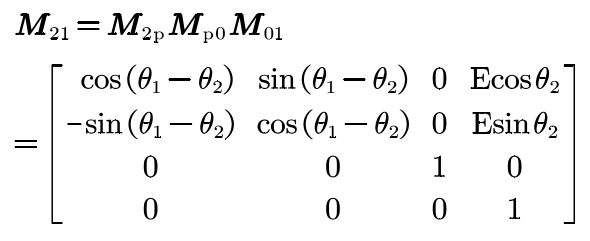
The parameter equation of the contact line R1 of the pinion in the coordinate system S1 is expressed as follows:
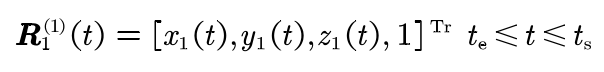
Where t is the variable parameter of space curve; Te and TS represent the corresponding values of the variable parameters of the contact line entering the meshing point and exiting the meshing point respectively. The superscript represents the coordinate system in which the vector is located, and the same representation will be adopted later.
Assuming that the contact point of space curve R1 and R2 at any meshing time is n (x1, Y1, z1), the relative velocity is reduced υ The expression of 12 in the coordinate system S1 is as follows:
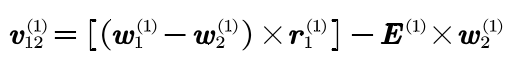
Where e is the vector from O1 to O2, and its module is the center distance E of linear gear pair. Each vector in the equation can be expressed in S1 as:
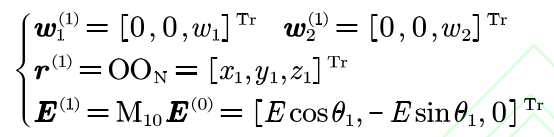
According to the meshing theory of space curve, the meshing equation of a pair of conjugate curves at any point is as follows
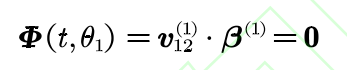
Where: υ 12 is the relative velocity of the space conjugate curve at the meshing point n; β It is the main normal deviation of the contact line on the pinion and ring gear at the contact point n
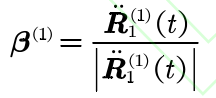
The rotation angle can be obtained from the formula θ And t
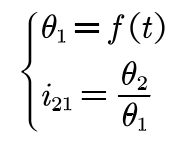
According to the formula, the parameter equation of the pinion contact line R2 in the coordinate system S2 can be obtained as follows:
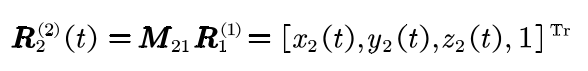
In order to obtain a pair of conjugate curves without relative sliding in the meshing process, it is necessary to ensure that the relative velocity of any meshing point is 0 in the meshing process
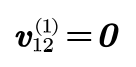
According to the formula, at any meshing moment, the relative velocity of meshing point n in S1 can be expressed as:
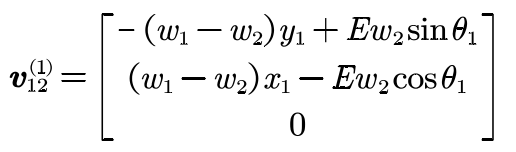
Through the formula, a pair of conjugate curves of pure rolling internal meshing parallel axis gear pair can be obtained.

