Abstract
This paper investigates the dynamic meshing characteristics of helical bevel gear pairs used in heavy-duty applications such as engineering and mining machinery. The analysis employs finite element methods to identify the effects of system damping, start-up acceleration time, and load on the dynamic meshing behavior and vibration response. An orthogonal experimental design and range analysis reveal the significance of each factor on gear vibration. The simulation results demonstrate that variations in damping coefficient and acceleration time significantly impact gear meshing stabilization time, while loading conditions primarily dictate post-meshing vibration amplitude. Excessive loads can deteriorate meshing quality, thereby affecting gear operational efficiency.
Introduction
Helical bevel gear is widely employed in high-performance applications due to their high contact ratio, enhanced load-bearing capacity, superior stability, and reduced noise levels compared to spur bevel gears. However, the complex tooth geometry and operating conditions can lead to vibrations and impacts during meshing, necessitating a detailed study of their dynamic behavior. This research focuses on analyzing the effects of various parameters on the dynamic meshing characteristics of helical bevel gear using finite element methods.
Literature Review
Several studies have examined the dynamic behavior of gears. Dai et al. [1] highlighted the impact of rotational speed on the dynamic characteristics of gear systems, proposing a new method for calculating dynamic mesh stiffness and analyzing its influence on system performance. Wen et al. [2] developed an analytical algorithm based on the slicing method for accurately and efficiently calculating bevel gear mesh stiffness, which was verified using finite element analysis. Jia et al. [3] investigated the effects of support stiffness and tooth surface coating on the meshing characteristics and fatigue life of automotive transmission helical gear pairs. Sun et al. [4] proposed a precise tooth profile model considering tooth profile asymmetry and processing parameters, validating its accuracy through finite element analysis and examining the influence of macro-geometric parameters on mesh stiffness.
However, a comprehensive analysis of the influencing factors on the dynamic meshing characteristics of helical bevel gear remains scarce, particularly in the context of heavy-duty applications. Therefore, this study employs finite element simulations to explore the effects of damping, acceleration time, and load on the dynamic behavior of helical bevel gear pairs.
Modeling and Simulation Methodology
1. Modeling of Helical Bevel Gear Pairs
1.1 Theoretical Background
Digital modeling enhances tooth surface accuracy and minimizes machining errors. This study derives the coordinate representations of each point on the helical bevel gear tooth surface based on existing theories and applies them to reconstruct the 3D model. The coordinate transformation method prevents meshing interference, as illustrated in Figure 1.
The rotation of an arbitrary point P1 on the tooth surface by θ1 corresponds to a rotation of θ2 = i21θ1 on the mating tooth surface P2. Using intermediate coordinate systems and rotation matrix transformations, the coordinates of each point on the mating tooth surface can be calculated.
1.2 Gear Parameters and 3D Modeling
Table 1 lists the specific parameters used for the helical bevel gear in this study.
| Parameter | Pinion | Gear |
|---|---|---|
| Number of Teeth | 20 | 48 |
| Face Width (b) | 28 mm | 28 mm |
| Module (m) | 3 mm | 3 mm |
| Pressure Angle (α) | 20° | 20° |
| Helix Angle | 10° | 10° |
| Dedendum Cone Angle | 21.188° | 64.408° |
| Face Cone Angle | 25.592° | 68.812° |
| Operating Cone Angle | 22.619° | 67.380° |
| Addendum Modification | +0.12 | -0.12 |
| Shaft Angle | 90° | 90° |
| Helix Direction | Left-hand | Right-hand |
The preliminary 3D model was created in SolidWorks, and the discrete points on the tooth surface were calculated using MATLAB. These points were then imported back into SolidWorks to refine the 3D model, as shown in Figure 2.
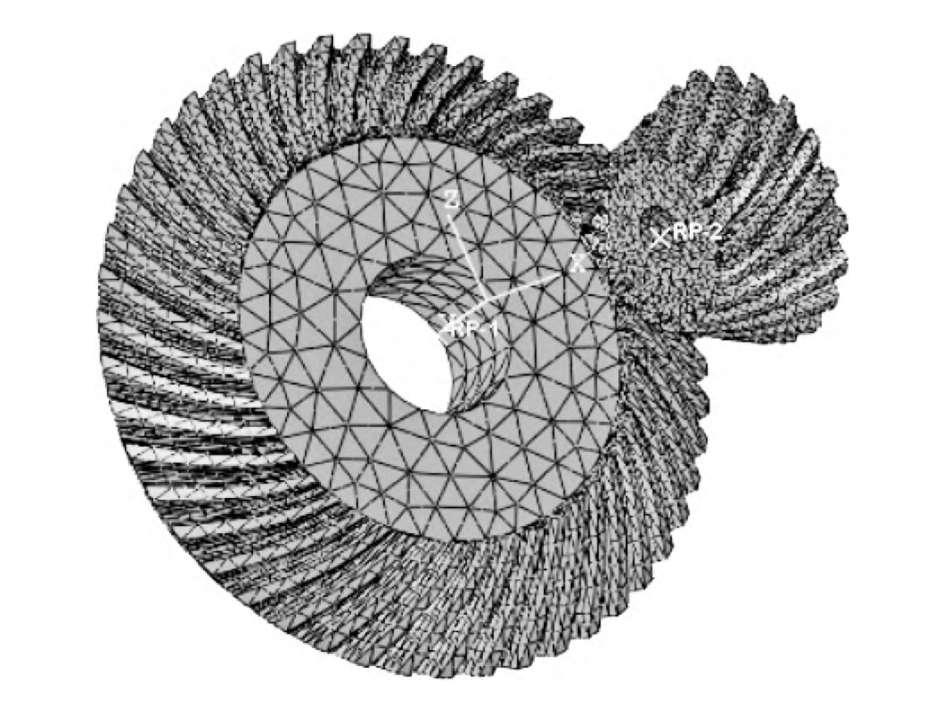
2. Finite Element Model Setup
2.1 Mesh Generation
The finite element model requires precise meshing to ensure accurate contact analysis. A fine tetrahedral mesh was used, with 26,752 elements for the pinion and 38,979 elements for the gear. The small sliding formulation was employed for contact interactions, and the Coulomb friction model was applied with a friction coefficient of 0.15.
2.2 Material Properties and Boundary Conditions
The gears were modeled using 45 steel with material properties listed in Table 2. The center reference points of the gears were coupled to the inner surfaces of their respective bores, and rotational speeds and torques were applied to these reference points. The pinion was set as the driving gear with a specified rotational speed, while the gear was loaded with a resistance torque.
| Material Property | Value |
|---|---|
| Elastic Modulus (E) | 209 GPa |
| Poisson’s Ratio (ν) | 0.269 |
| Density (ρ) | 7,900 kg/m³ |
| Thermal Conductivity | 48 W/(m·K) |
| Coefficient of Thermal Expansion | 1.3×10⁻⁷ K⁻¹ |
3. Model Validation
The accuracy of the finite element model was verified using Hertzian contact theory, which calculates the stress distribution between two elastic bodies in contact. Five points along the contact line were selected as reference points, and the maximum contact stresses were compared between analytical and finite element results (Table 3).
| Serial No. | Analytical (MPa) | FEA (MPa) | Relative Error (%) |
|---|---|---|---|
| 1 | 1018.63 | 990.32 | 2.80 |
| 2 | 1022.98 | 1000.22 | 2.23 |
| 3 | 1031.62 | 1003.42 | 2.74 |
| 4 | 1042.27 | 1013.62 | 2.75 |
| 5 | 1054.75 | 1015.8 | 3.69 |
The results show that the relative errors are below 10%, confirming the reliability of the finite element model for subsequent dynamic meshing analysis.
Analysis of Dynamic Meshing Characteristics
3.1 Effect of Damping
Damping significantly influences the dynamic meshing behavior. Three models were created with damping coefficients of 400, 600, and 800 N·s/m, while keeping other parameters constant. Figure 6 depicts the angular velocity variations of the gear under different damping conditions.
The results indicate that higher damping coefficients shorten the stabilization time, with a 60% reduction from 0.0136 s (400 N·s/m) to 0.0096 s (800 N·s/m). However, damping does not affect the stable rotational speed.
3.2 Effect of Acceleration Time
The acceleration time of the pinion affects the dynamic loading and stress during start-up, influencing gear life and reliability. Three acceleration times (0.001 s, 0.003 s, and 0.005 s) were analyzed while maintaining other parameters.
Shorter acceleration times result in faster initial angular velocity changes but higher impact forces. The stabilization time increases from 0.004 s to 0.084 s as acceleration time doubles from 0.001 s to 0.005 s.
3.3 Effect of Load
Load variations significantly impact vibration and stress levels. The gear was loaded with torques of 200, 400, and 800 N·m, while other parameters remained unchanged.
Higher loads increase the amplitude and frequency of angular velocity fluctuations, necessitating careful load selection to avoid excessive vibrations. Load variations do not significantly affect stabilization time.
3.4 Orthogonal Experimental Design and Range Analysis
An orthogonal experimental design (L9(3³)) was employed to analyze the combined effects of damping (A), acceleration time (B), and load (C) on angular velocity and contact stress. Table 4 lists the factor levels, and Table 5 shows the experimental results.
| Level | Factor A (Damping, N·s/m) | Factor B (Acceleration Time, s) | Factor C (Load, N·m) |
|---|---|---|---|
| 1 | 400 | 0.001 | 200 |
| 2 | 600 | 0.003 | 400 |
| 3 | 800 | 0.005 | 800 |
| Serial No. | Parameter Combination | Average Angular Velocity (rad/s) | Maximum Contact Stress (kN) |
|---|---|---|---|
| 1 | A1B1C1 | 32.31 | 99.91 |
| 2 | A1B2C2 | 39.24 | 103.19 |
| … | … | … | … |
| 9 | A3B3C2 | 34.27 | 138.62 |
Range analysis reveals that damping has the most significant impact on angular velocity stabilization, while load primarily influences maximum contact stress.
Conclusion
This study comprehensively analyzed the dynamic meshing characteristics of helical bevel gear pairs using finite element methods. The key findings are:
- Damping: Increasing damping coefficients shorten the stabilization time significantly without affecting the stable rotational speed. Higher damping ensures faster stabilization of the gear system.
- Acceleration Time: Longer acceleration times reduce initial impact forces and angular velocity fluctuations, leading to smoother speed changes and improved meshing quality.
- Load: Load variations primarily affect the amplitude and frequency of post-meshing angular velocity fluctuations. Excessive loads can deteriorate gear performance, necessitating careful selection based on operational requirements.
The analysis provides valuable insights into the dynamic behavior of helical bevel gear and can guide the design and optimization of gear systems in heavy-duty applications. Future research could explore the effects of pinion rotational speed and contact stress variations under different conditions.
