In the past 30 years, a large number of scholars have used finite element, experimental analysis and theoretical calculation to analyze the meshing stiffness of helical gears. Andersson and vedmar first calculated the dynamic load of the helical gear, and calculated the time-varying meshing stiffness of the helical gear by using the finite element method. In the calculation process, the tooth deformation obtained from the experiment was taken into account, so that the calculation results were closer to the actual situation of the helical gear. S. Baud and p.velex used the finite element method to calculate the load distribution of spur gears, and analyzed the influence of load distribution and meshing error on the meshing stiffness of helical gears. The contact problem of helical gear tooth surface is often solved by analytical methods such as material mechanics and elastic mechanics. Usually, two meshing helical gears are simplified into two cylinders, and the contact deformation and contact stress of helical gears are calculated by Hertz theory. It is considered that the finite element method is often used to calculate the deformation and stress of complex structures, and it is often used to calculate large coincidence gear (hcrg) in helical gear calculation. Based on the elastic deformation matrix of the meshing region and combined with the finite element method, Tengjiao Lin and Runfang Li analyzed the meshing stiffness of helical gears in the three-dimensional meshing region.
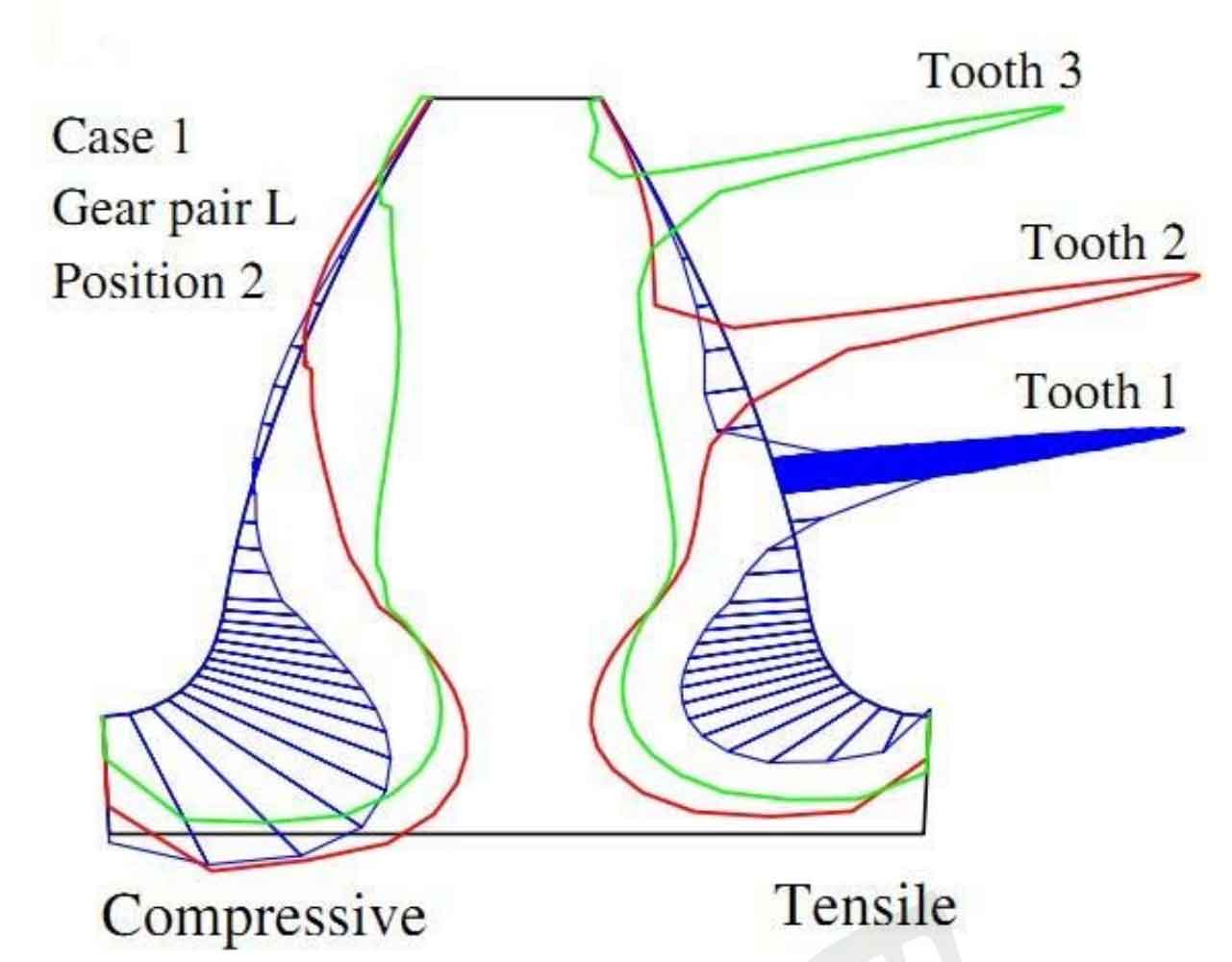
The calculation of meshing deformation and time-varying meshing stiffness of helical gears is an important part of helical gear dynamics research, which has been the focus of scholars at home and abroad. Shuting Li uses the tooth contact model and the finite element method to analyze the helical gear deformation and stress calculation. The analysis results show that the stress distribution along the tooth profile direction is asymmetric. Figure 1 shows the distribution of bending stress along the tooth profile direction.
Ignacio Gonzalez Perez and others believe that the finite element method is very effective in analyzing the maximum contact stress and stress distribution of helical gears, which provides a more convenient algorithm for the dynamic calculation of meshing deformation of helical gears. Song he et al. Considered tooth modification in static modal calculation, and built an accurate finite element contact model to calculate each instantaneous stiffness within the load working range.
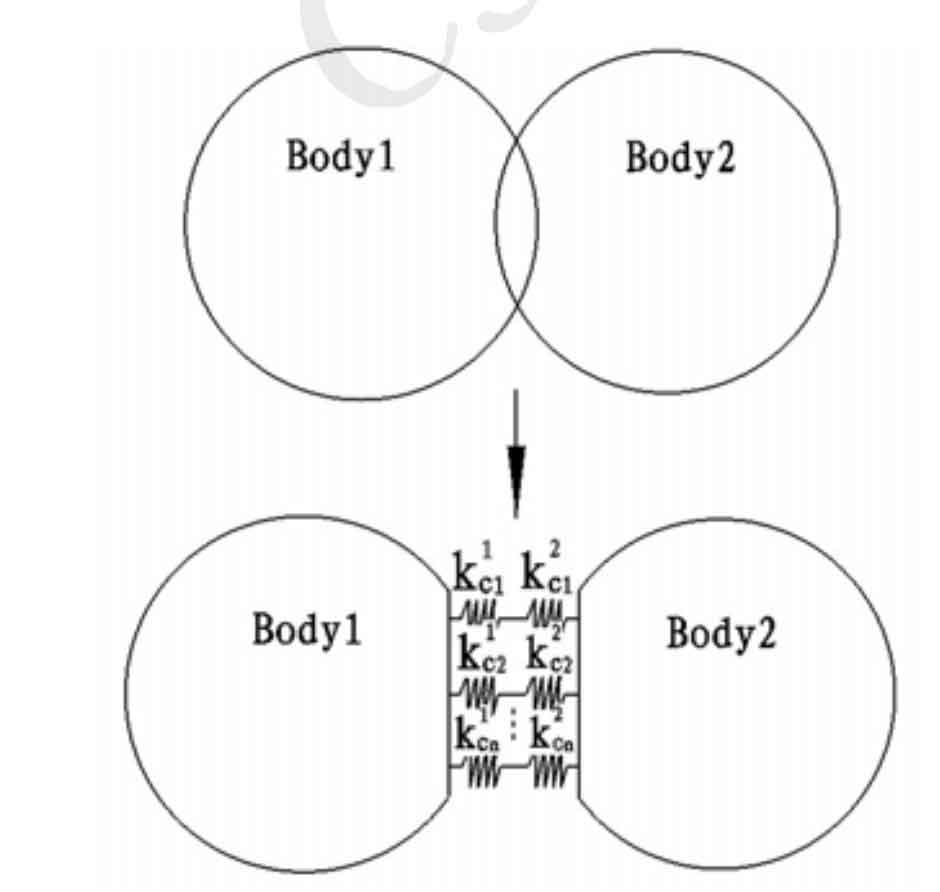
Monsakpimsarn and Kazem kazerounian put forward a new method to calculate the meshing stiffness of helical gears, which simplifies the gear teeth into an elastic contact problem as shown in Figure 2. The calculation speed is much faster than the finite element contact calculation to calculate the coincidence degree of rigid bodies, the contact force on the meshing surface and the singular stiffness at the contact point.
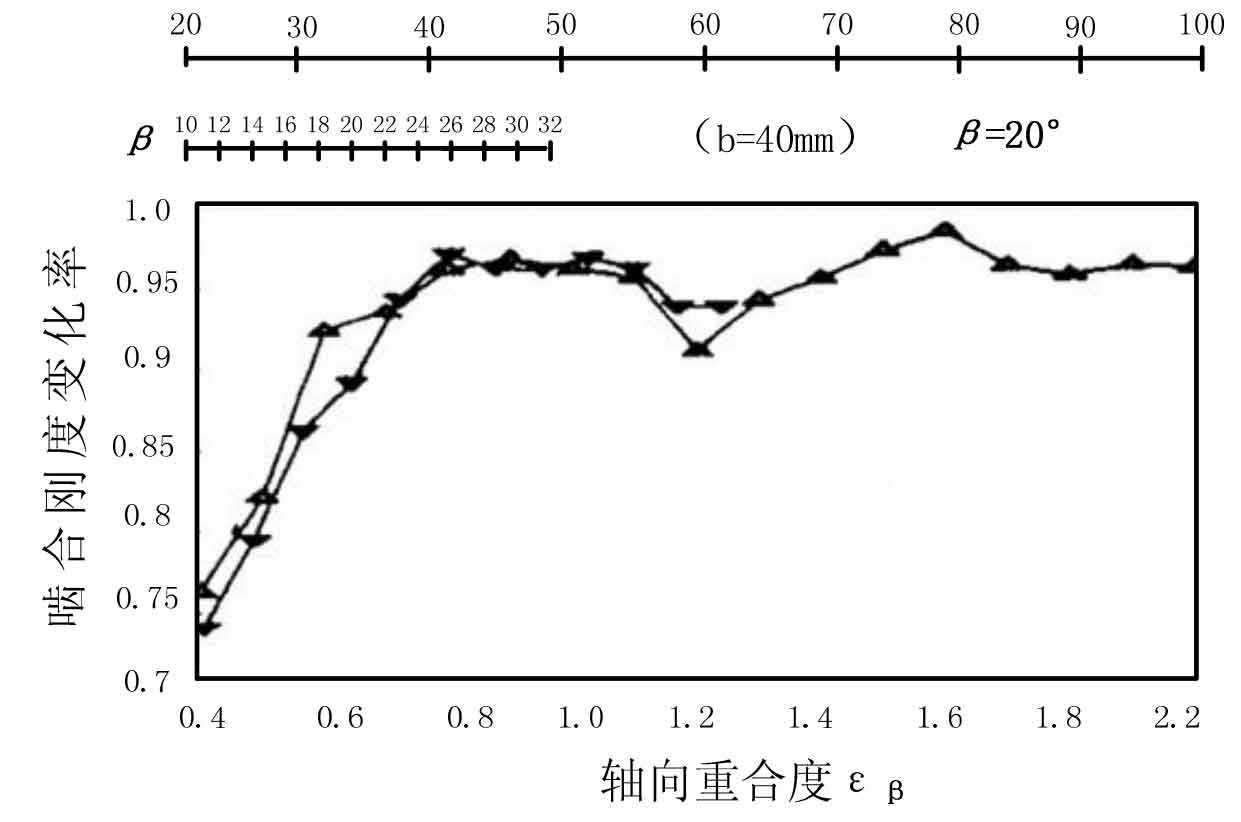
Changshan et al. Used the finite element flexibility matrix method to consider the influence of the helical gear matrix deformation on the tooth stiffness, and obtained the relationship curve between the change rate of the instantaneous meshing stiffness and the axial coincidence degree of the helical gear in the meshing process, as shown in Figure 3:
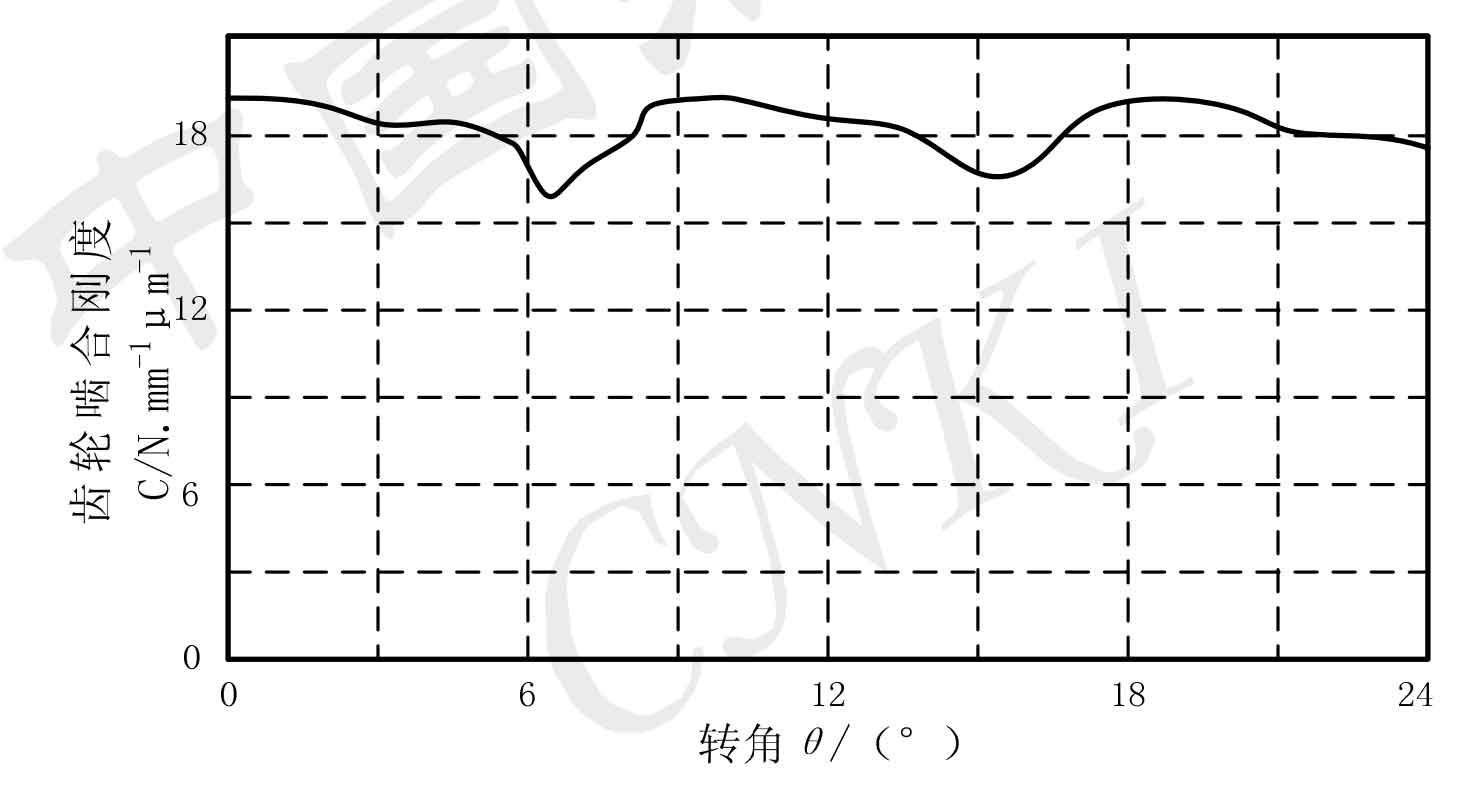
Lintengjiao et al. Used the meshing principle and finite element method to automatically model and determine the position of the meshing point, used the finite element method to calculate the time-varying meshing stiffness of the helical gear, and was able to determine the tooth surface load distribution and the time-varying meshing stiffness change curve. Figure 4 shows the curve of the time-varying meshing stiffness of the helical gear changing with the gear angle.
Fakher chaari et al. Built an analysis model of helical gear meshing stiffness considering the tooth crack of helical gear, and analyzed the influence of tooth crack on meshing stiffness. On the basis of considering the tooth deformation and meshing error, Tang Jinyuan et al. Analyzed the contact outside the meshing line of the tooth, and put forward the calculation method of the stiffness of the helical gear with out of line meshing.
