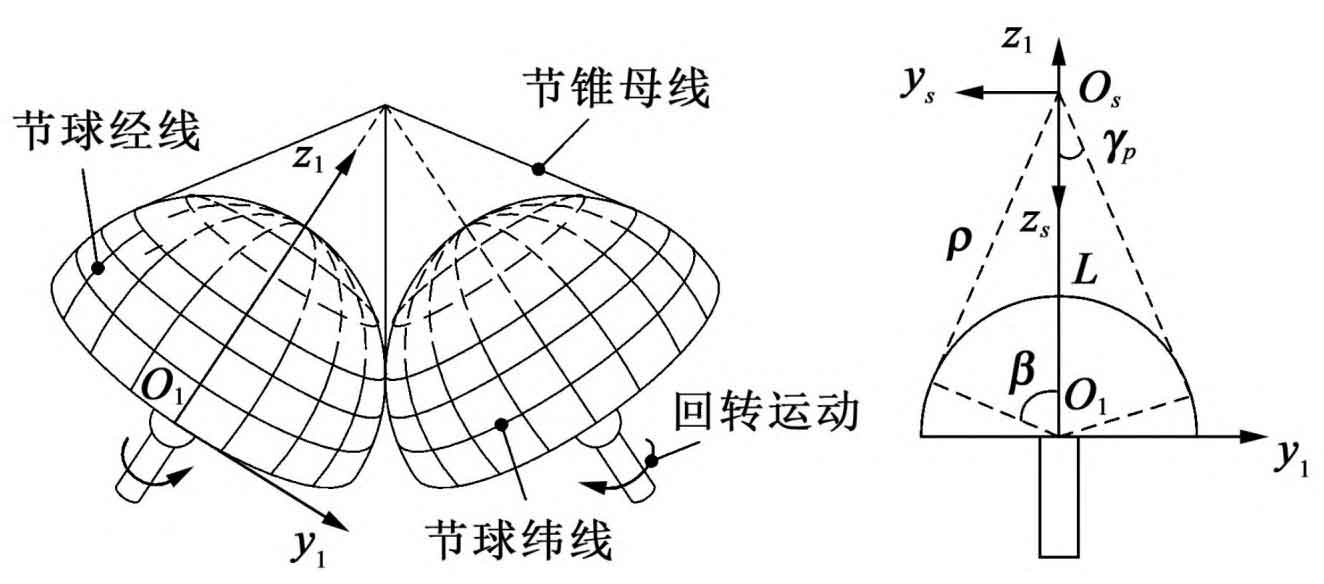
As shown in Figure (a), the pure rolling between a pair of pitch cones is equivalent to the meshing motion between spherical involutes of arc tooth surfaces. Under the condition that the transmission ratio is 1 ∶ 1, a pair of pitch cones follow the pitch ball from the dotted line position in Figure (b) until the two cone generatrix coincide.
In the coordinate system (O1, x1, y1, z1), the arc tooth surface equation is:
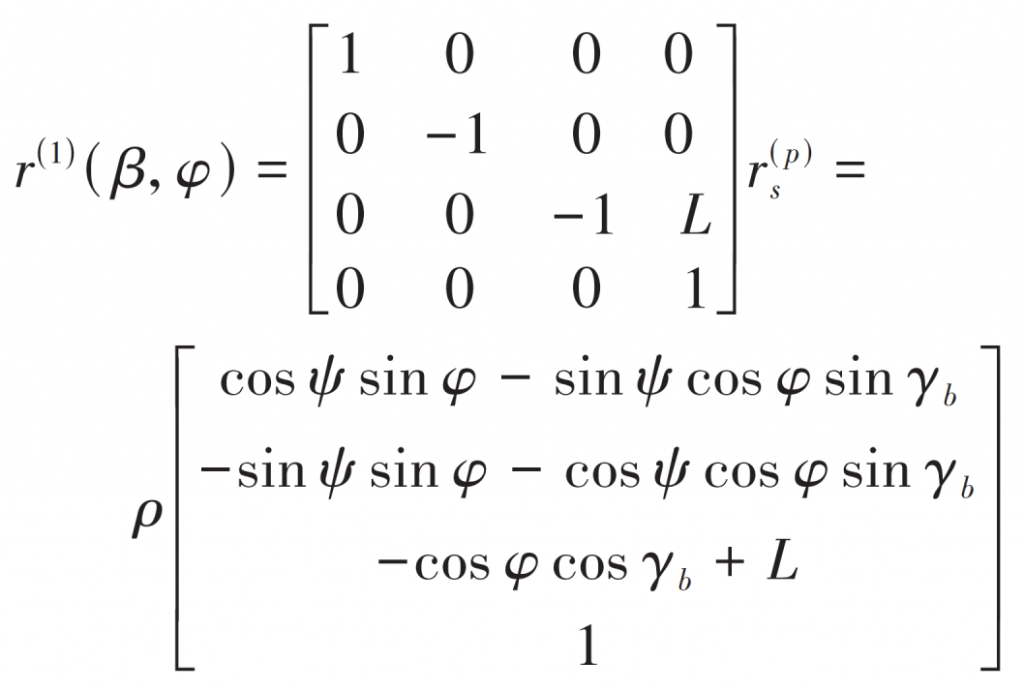
Where, ρ Is the length of the tapered busbar in Figure (b); L is the distance from point Os to point O1; φ It refers to the rolling angle of circular plane during the formation of spherical involute. The other variables are the same as the parameters of the spherical involute equation; ψ Is spherical involute rolling angle.
According to the formula, the parameters of arc tooth surface are β And φ,β Is the pitch angle of the pitch cone on the spherical surface in Figure (b), which is determined by the pitch circle and the number of teeth of the hemispherical bevel gear.
The rigid body dynamics equation of the hemispherical bevel gear is a pair of gear meshing motion, so the conjugate meshing equation needs to be established. The conjugate meshing equation has been discussed in detail. Due to space limitation, only the main reference formula is given here:
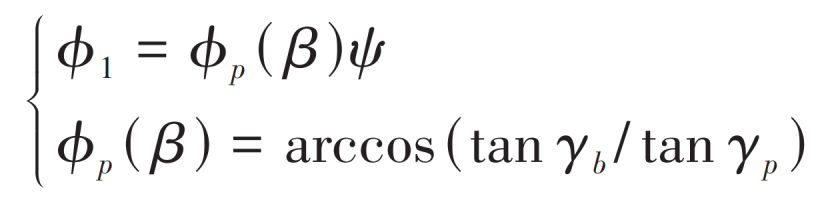
Where, γ B is the base cone angle; γ P is the coning angle.
