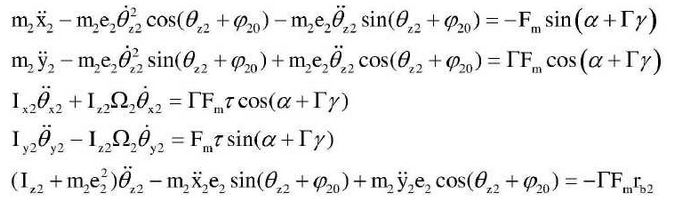Lagrange method is used to establish the yaw-torsion coupling nonlinear dynamic model of fixed-axle gear drive. The Lagrange equation is:
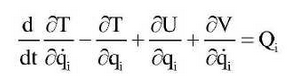
In the formula, T, U and V are respectively kinetic energy function, potential energy function and energy dissipation function; Qi is the general coordinate of their degrees of freedom, Qi is the general velocity of their degrees of freedom; Qi is the non-conservative general force except the viscous dissipation force.
1.Kinetic energy function
First-order derivation of the position vector of each gear center obtained from the formula with respect to time indicates that the translation speeds R1 and R2 of each gear center are respectively:
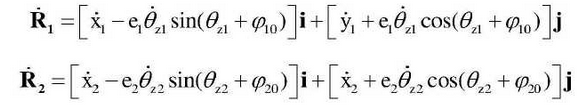
Tooth offset moment or gear offset to one side without the center position of the shaft will change the spatial orientation of the rotating shaft of the gear and cause gyroscopic effect.Considering the influence of gyroscopic effect, the kinetic function of fixed-axle gear drive is obtained from the translation speed, rotation speed and swing speed of each gear centroid position as follows:
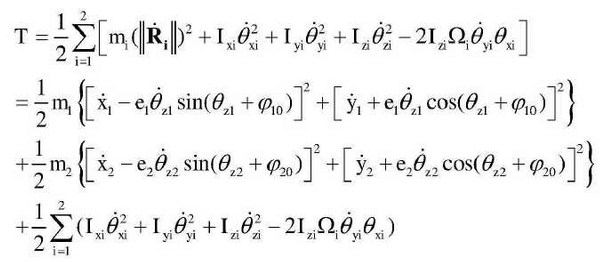
Where Ω is the theoretical gear speed, i=1,2.
The modeling process is only for fixed-shaft gear drives and elastic elements such as drive shafts and bearings are not considered, so the potential function U and the energy dissipation function V are equal to 0.
2. Non-conservative generalized forces
For gear drives, non-conservative generalized forces are mainly generated by gear pair engagement.Whether the tooth surface or back engages, the engagement force always follows the engagement line and points to the extension line, and the bias moment is always perpendicular to the engagement plane.A positive counterclockwise direction is defined in the direction of torsion.As shown in the figure, force analysis is carried out on the meshing state of tooth surface and back, and column vectors composed of non-conservative generalized forces acting on each generalized coordinate are represented as follows:
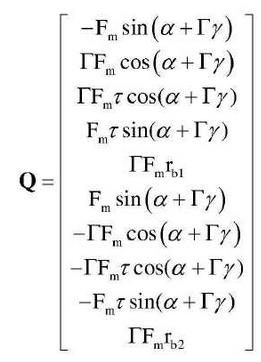
In the formula, Fm is the dynamic engagement force; the engagement state of tooth surface Γ=1 and the engagement state of tooth back Γ=-1, in which the engagement state of tooth surface and tooth back is determined by the clearance function; α is the dynamic engagement angle; γ is the relative position angle; τ is the offset.
3. Nonlinear dynamic model
By substituting the kinetic energy function formula and the non-conservative generalized force formula generated by gear meshing into Lagrange function, the non-linear dynamic equation of yaw-torsion coupling of fixed-axle gear drive is obtained.
The dynamic equation of gear 1 is:
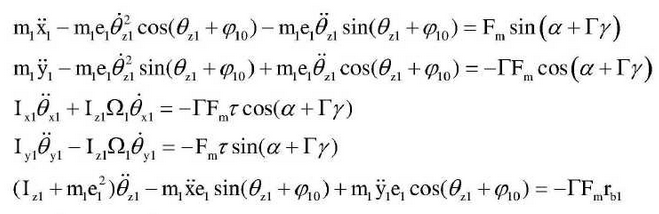
The dynamic equation of gear 2 is: