Helical gears are meshed at the same time in the process of meshing. When studying the dynamic problem of gear pair considering backlash, it is assumed that there is only torsional vibration in the center of two gears in the gearbox system, while the transverse vibration is ignored; the direction of the meshing force between the teeth always coincides with the common normal line at the contact point of the two tooth surfaces. In this way, the contact problem between tooth surfaces is simplified as the connection of spring and damping, expressed by damping coefficient and spring stiffness coefficient respectively. But in the actual meshing process, due to the influence of transmission error, the meshing force is not in the direction of the meshing line. The dynamic model of gear meshing is shown in Fig. 1.
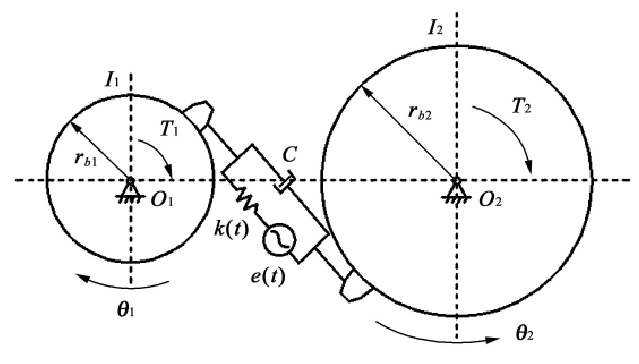
After the gear pair is simplified to the dynamic model shown in Fig. 1, the displacements of the driving gear and the driven gear on the meshing line are defined as X1 and X2 respectively according to Newton’s classical mechanical method
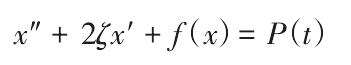
Where, ζ = C / 2m ω n; C is the damping coefficient of gear meshing; m is the equivalent mass of gear pair; ω n is the natural frequency of gear dynamic model; P (T) = PE (T) + pH (T), PE (T), pH (T) are dimensionalized internal and external excitation respectively; f (x) is the meshing force function between teeth with backlash.
Due to the error accumulation during manufacturing and installation, in order to prevent the gear from displacement and deformation, there is a gap between the teeth to ensure the normal lubrication of the tooth surface. There are two ways to increase the side clearance: one is to increase the distance between the driving and driven shaft holes on the gearbox before installation; the other is to reduce the tooth thickness during manufacturing. The second method is easy to control the size of the side gap, because the machining of the box is generally based on rough datum, and the accuracy is difficult to guarantee.
If the backlash of gear pair is 2B, the piecewise function of backlash in nonlinear dynamics of gear is expressed as follows:
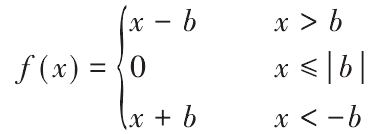
Where, f (x) is the meshing force between teeth with backlash; B is the clearance on one side of the gear; X is the displacement of the driving wheel and the driven wheel on the meshing line; when x > b, the driving wheel contacts with the driven wheel and transmits the torque to the driven wheel, which is the process of deceleration and meshing; when – B ≤ x ≤ B, the two gears do not contact and do not transfer torque; x < – B It is the process of increasing speed meshing. Because the deformation of the driving wheel and the driven wheel are affected by each other, it changes constantly when the tooth surface is meshed. The meshing process is mainly the repeated process of tooth surface contact, collision and separation.
