1 Introduction
As a key part in mechanical transmission, bevel gear is widely used in aviation, aerospace, automobile and construction machinery transmission, and its tooth surface quality is an important indicator to measure the performance of meshing transmission. In bevel gear three
In dimensional measurement, the traditional method of 45 discrete grid points for contact measurement is inefficient, and it is difficult to obtain full tooth surface data. With the wide application of optical measurement technology in gear measurement, the problem of insufficient tooth surface measurement points is effectively compensated. For bevel gear quality, it can be used
Theoretical calculations are used for evaluation, but often rely on complex mathematical models of bevel gears. The model is influenced not only by bevel gear design parameters, but also by machine tool adjustment parameters. In the actual bevel gear
In quality evaluation, process parameters are often difficult to obtain, and the theoretical mathematical model of tooth surface is difficult to establish, so the relativistic evaluation method is an ideal choice.
In this paper, the three-dimensional tooth surface information of bevel gears is obtained by optical measurement method, and a relativized evaluation method for bevel gear quality is studied, which overcomes the dependence on complex theoretical models in traditional bevel gear measurement and obtains information The problem of insufficient interest rate further reflects the stability of the bevel gear production process at the processing site.
2 Principle of relative method assessment
2.1 Bevel gear theoretical tooth flank
Figure 1 shows the three-dimensional coordinate system of the bevel gear, the z-axis of the coordinate system coincides with the rotary axis of the bevel gear, the xOy plane is perpendicular to the z-axis and coincides with the end section of the large end of the bevel gear, and the origin O is located at the z-axis and the major end of the gear The intersection of polygons. The tooth surface equation for bevel gears can be expressed as

2.2 Establish the reference tooth surface
A workpiece gear with better tooth surface quality is selected as the reference gear from the same batch of bevel gears, and the three-dimensional data point set of the tooth surface can be expressed by a discretized mathematical model. As shown in Figure 2, take the two directions of U and V on the tooth surface and establish a coordinate system, where the U direction is pointed from the root to the tooth top, and the V direction is from the large end of the bevel gear to the small end. The coordinate W is used to represent the serial number of each tooth. Based on the special U-V-W coordinate system described above (see Figure 2), the discretized point cloud data of the ipsilateral tooth flank of the datum gear can be represented in a structured 3D model, as shown in Figure 3.
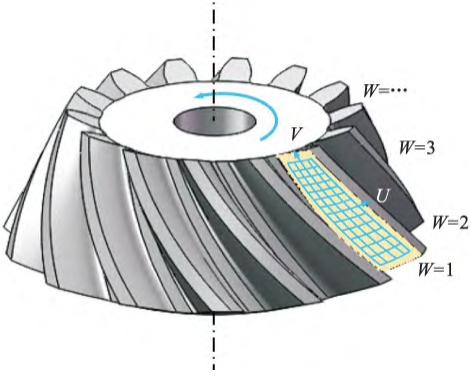
Figure 1 Gear coordinate system
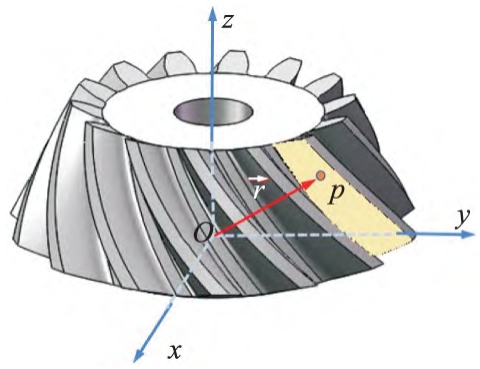
Figure 2 shows the three-dimensional tooth flank Special U-V-W coordinate system
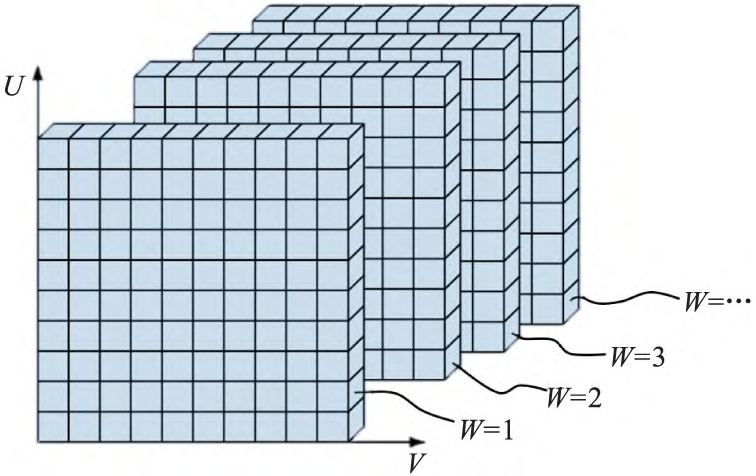
Figure 3 Structured 3D model of tooth surface data
The subscripts i,j,k represent the serial numbers of the discretized data points in the three directions of U, V, and W, respectively, and pi, j, k represent the points on the tooth surface with coordinates of (i,j,k), where i = { 1,2,…,m} , j = { 1,2,…,n} , k = { 1,2,…,
l} , m, n , l are the number of data points in the direction of U, V, and W, respectively, and are off
The scattered bevel gear tooth surface information can be recorded as the following three-dimensional array, there is
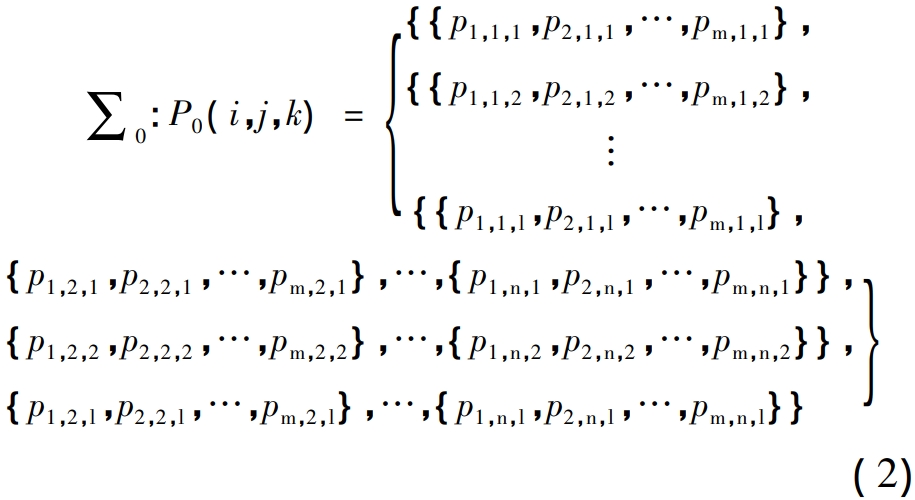
After homogenizing each tooth surface of the reference gear, it can be used as the reference tooth surface, and the three-dimensional point set of the tooth surface can be expressed as
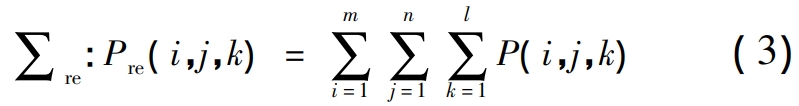
The datum tooth surface is fitted by the NURBS surface fitting method, and the NURBS surfaces of g degree in the U direction and h degree V have a bivariate piecewise rational vector function [4] form
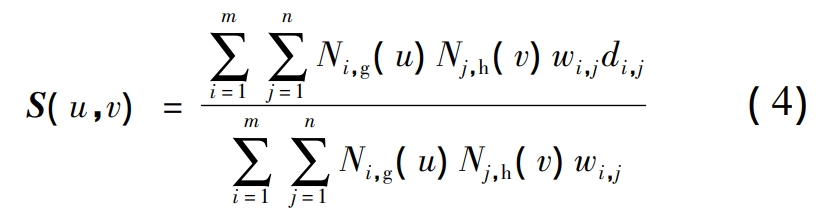
It can also be expressed as

where di, j are the vertices of the control mesh; wi,j is the weight factor; Ni,g ( u) ,
Nj,h ( v ) are non-rational B-spline basis functions defined on the node vectors you and V, respectively. Therefore, the unit vector of p at any point on the datum tooth surface can be tabled
Shown as
At this point, the direction of the unit normal vector is from the reference tooth face to the actual tooth surface.
2. 3 Relativization evaluation obtains three-dimensional tooth surface information of bevel gears by optical measurement methods, and the data point set of the actual gear can be represented as
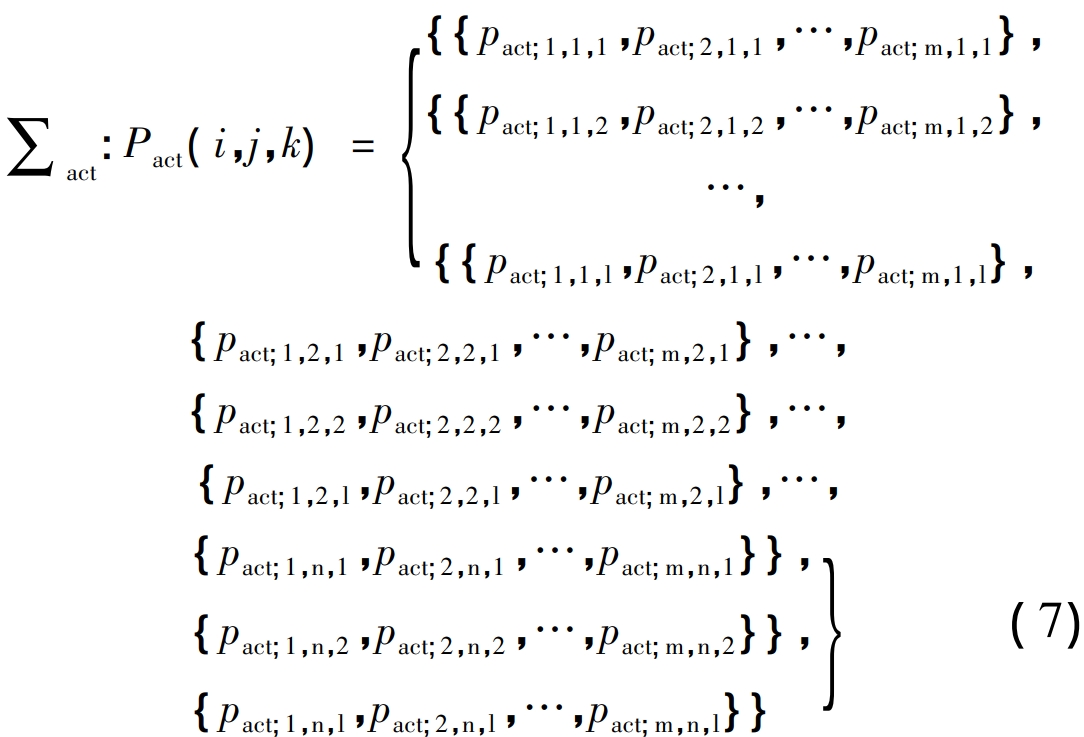
As shown in Figure 4, the actual flank and the datum flank are placed at the same location in the gear coordinate system for relativized comparison.
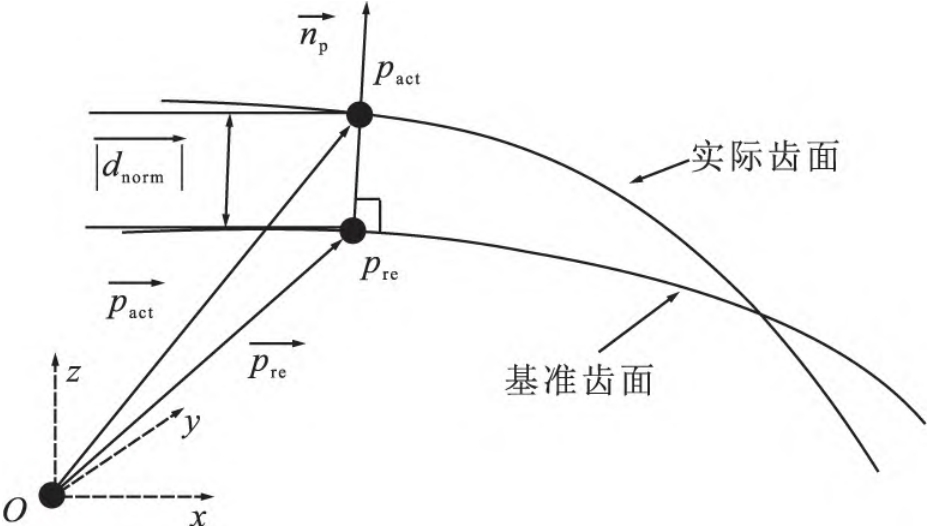
Figure 4 Tooth flank normal deviation
The relationship between the actual tooth surface and the corresponding point of the reference tooth surface satisfies equation ( 7), there is
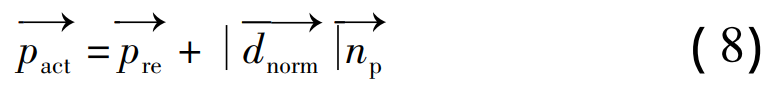
Therefore, it can be determined that the normal deviation of the actual tooth flank relative to the reference tooth flank is
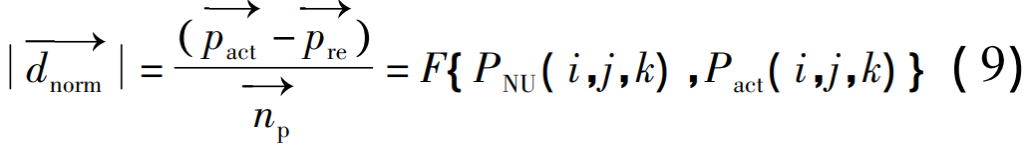
3 Gear 3D measurement system
Figure 5 shows a bevel gear three-dimensional measurement experiment device equipped with a line structured light sensor mounted on the gear measurement center. The gear under test is mounted on the instrument rotary spindle and rotates with the spindle at a certain speed. The linear structured light sensor is mounted on the linear motion axis base by means of a fine-tuning platform, which can realize the adjustment of any position in space. During the measurement process, the rotation angle signal of the spindle is used as an external trigger source to trigger the sensor acquisition signal, and the contour acquisition data of the tooth surface is obtained in real time. The sensor uses the KEYENCE LJ – V7000 series line structured light sensor with a nominal distance of 60mm and a measuring range of 13 line width. 5 ~ 15mm, height measurement range of ± 8mm and repeatability of 0. 4μm。 As shown in Figure 6, a 9-tooth arc-tooth bevel gear is selected for the gear under test, and the basic parameters are shown in Table 1.

Figure5-wire structured light gear 3D measurement system Figure 6 The gear under test
Establish the coordinate system of the measurement system shown in Figure 7, where Og -xg yg zg is the gear coordinate system, O0 – x0 y0 z0 is the world coordinate system, and Os- xsyszs is the sensor coordinate system. The gear coordinate system ZG shaft coincides with the gear axis and rotates with the gear; The world coordinate system z0 axis and origin O0
Coincident with the gear coordinate system zg axis and origin og, respectively; The sensor coordinate system origin Os is located at the center point of the outgoing laser line, and the plane xsOsys is parallel to the laser plane.
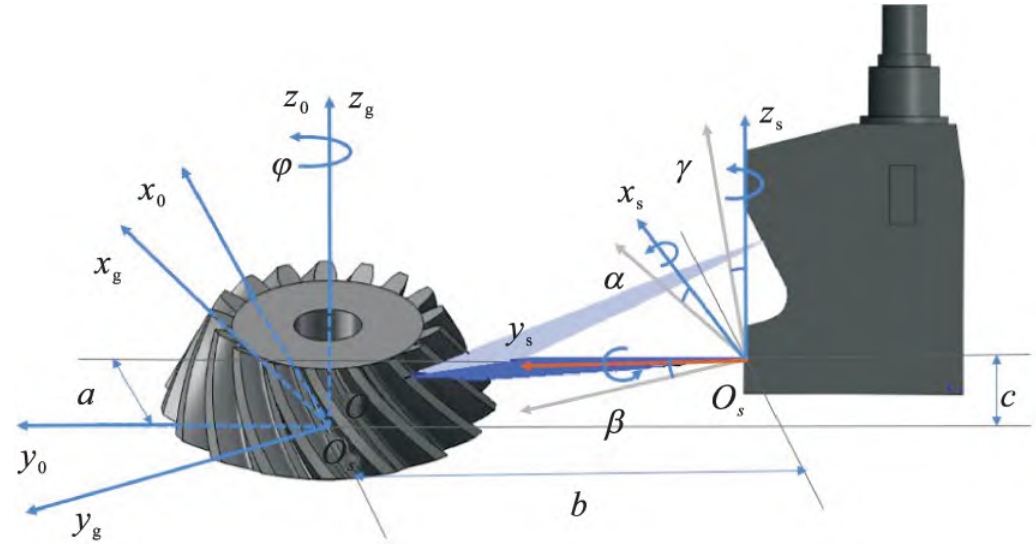
Figure 7 Coordinate relationships
The measured 3D tooth surface data of bevel gears can be obtained through the line structured light gear measurement model

where Dg,act is the coordinate value of the measured point in the gear coordinate system, Dg,act= xg,act,yg,act,z ( ) g,actT; The matrix gMs is about the gear angle φ and the transformation moment of the sensor pose parameter [α,β,γ,a,b,c][5];
Ds is the coordinate value of the measured point in the sensor coordinate system, Ds = xs,y ( ) s,zsT.
4 Experimental verification
4.1 Datum tooth surface acquisition
A workpiece gear with better quality is selected from a batch of arc bevel gears with the same parameters as the reference gear, and the 9 tooth surfaces of the reference gear are used as the reference tooth surface, and the three-dimensional data point cloud is shown in Figure 8.
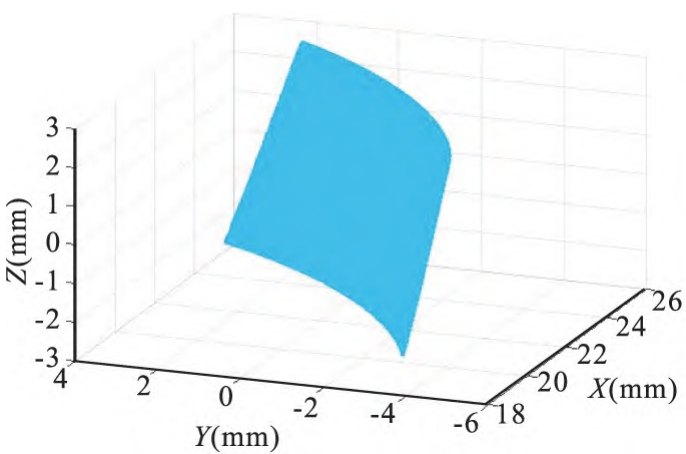
Figure 8 Datum tooth flank
4.2 Obtain the tooth surface to be measured
The measured gear is measured in the bevel gear three-dimensional measurement experimental device, the original data of the actual tooth surface of the gear is obtained, and the three-dimensional point cloud of the measured arc tooth bevel gear is obtained by coordinate transformation, as shown in Figure 9.
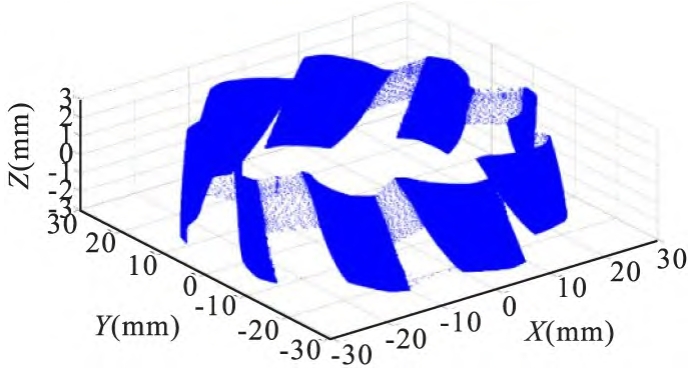
Due to the bias of the linear structured light sensor in the x-axis direction, only one tooth flank can be measured at a time due to the curvature of the tooth flank of the arc bevel gear and laser rereflection. The experiment chose to measure the convex surfaces of the arc bevel gear teeth, each with approximately 3.2 million points. In addition, the actual 3D point cloud data of the gear is affected by the sensor’s laser beam width and spatial pose, and the z-axis direction data is concentrated between -3mm and 3mm. Point cloud data of the full tooth flanks on both sides of the arc bevel gear can be obtained by moving the sensor symmetrically in the x-axis and equidistant along the z-axis. According to the division rule of the tooth surface evaluation area of the arc bevel gear (the top and bottom ends of the tooth are located at 5% of the tooth height in the direction of the tooth profile, and cannot exceed 0.6mm), the evaluation area of the original point cloud data is extracted and the high-frequency interference is filtered. The actual tooth surface evaluation area is shown in Figure 10.
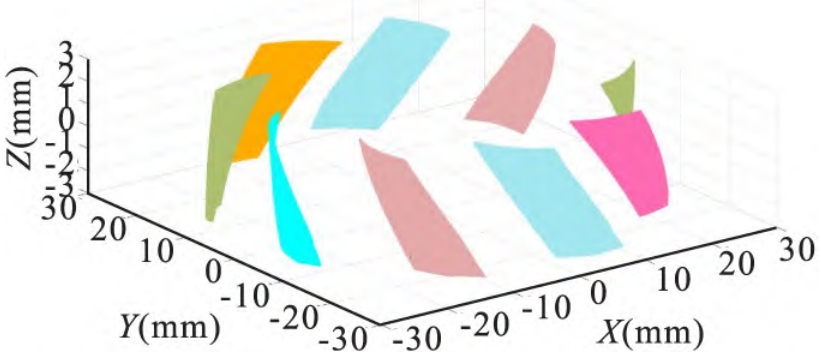
Figure 10 Actual tooth surface evaluation area
4.3 Deviation calculation and analysis
In order to facilitate the comparison and analysis of the actual tooth flank with the reference tooth flank, all discrete points of the tooth flank are projected onto the axial profile. By matching the point cloud coordinates of the datum tooth surface with the actual tooth face, the actual tooth surface is compared relative to each other
The normal deviation of the reference tooth surface (see Figure 11) has a maximum normal deviation value of 2. 166μm with a minimum normal deviation value of – 2. 284μm。

Figure 11 Comparison of tooth surface relativization
Five bevel gears with the same parameters of the batch were randomly selected for relative quality evaluation, and the normal deviation results are shown in Table 2. It can be seen that the relativity evaluation results of the selected gear are well consistent
It further reflects that the production process of this batch of bevel gears has good stability.
5 Conclusion
In this paper, a three-dimensional measurement of arc bevel gear is studied in view of the difficulty of theoretical tooth surface construction caused by the difficulty of obtaining process parameters and complex adjustment parameters of machine tools in the quality evaluation of actual bevel gears
Relativized assessment methods. In this method, a workpiece gear with high quality of the same batch is selected as the reference gear, and the homogenized tooth surface of the reference gear is used as the reference tooth surface. Combined with line structured light gear three-dimensional measurement technology
, obtain richer actual three-dimensional tooth surfaces, and compare and analyze with the reference tooth surfaces, and then obtain the normal deviation and evaluation results of the measured gear. Experimental results show that the bevel gear quality relativization method is an ideal solution when it is difficult to construct theoretical tooth flanks, which not only overcomes the complex theory of bevel gear dependence in traditional measurement
The problem of insufficient information obtained by the model can also reflect the stability of the bevel gear production process at the processing site while evaluating the quality of the gear. In future research, the information collection and quality evaluation of full tooth width should be expanded to better characterize the quality of the full tooth surface and reliably monitor the stability of the process at the production site.
