Aviation fuel system and stable and powerful propulsion for enginesClosely related, as a main component of the fuel system, aviation fuel gear pumpThe performance directly affects the stability and reliability of engine operation. WithThe fuel gear pump is gradually developing towards high speed and high power,bring a series of problems such as reduced volumetric efficiency, flow fluctuation, vibration noise, etc.These problems have seriously hindered the improvement of the performance of fuel gear pumps, and scholars have made efforts to solve these problems.A lot of research has been done to explore the effect of high speed and low viscosity medium on theThe reliability of dynamic pressure lubrication for sliding bearings in line gear pumps is analyzed by considering the lubrication characteristics and contact behavior of sliding bearings in gear pumps. Through numerical analysis of double-arc helical gears using Fluent, the sameComparisons of flow characteristics of involute helical gear pumps under different geometric parameters were conducted. A study was conducted on the CCHGP type gear pump, based on the lumped parameter methodThe fluid mechanics of the gear pump can reduce or even eliminate flow pulsation.
In terms of the influence of gear tooth profile and speed on pump flow characteristics:Analyze the eccentricity of gears for different gap shapes and sizesThe impact of leakage and pressure accumulation on the circumference. ThroughMulti-objective optimization method for determining the size of the gear and the flow change mechanism, used forAnalyze the instantaneous flow rate and flow non-uniformity of the pump. It is concluded thatPumps with larger modulus, larger face width or smaller number of teeth have larger displacement,But it may lead to more serious flow rate fluctuations. For different teethThe flow pulsation of a number of external gear pumps was studied, and it was concluded that the increase in tooth numberThe conclusion that the flow quality of gear pump can be improved, and establish the gearThe dynamic model of pressure pulsation during the single and double tooth meshing process of the pump, discusses the rotationThe modulation effect of frequency on pressure pulsation signals and the influence of different operating conditions on pressure pulsationThe impact of dynamic factors. With the development of various computer-aided software and various experimental methods,It is increasingly perfected, and the non-circular gear variable speed drive is proposed to stabilize the square wave.analyzing the composition of flow pulsation in elliptical gear pumps. By using waveletThe finite element method is used to simulate multiple cracks on the gear of the gear pump for identification.The location and size of multiple cracks on the gear pump gear. Cylindrical Gear Through trial and error,Test and evaluate the model to determine the internal pressure evolution of the external gear pump tooth spaceVariable excitation load.
At present, in order to meet the high reliability requirements of aviation fuel gear pumps in extreme environments,Requirements for performance and high stability, the structure of the main component gear in the gear pumpDevelop towards multi-tooth and spiral direction, and try it out in the production of circular arc gear pumpIn the process of research, we found that the number of gear teeth has a great influence on its performance. Therefore,Cylindrical Gear this articleTaking the circular arc fuel gear pump as the research object, the tooth crest and tooth root of the gear pumpA smooth arc is used, with the middle connected in an involute manner, to study the teethThe influence of the number on the flow characteristics in the gear pump cavity. The structure of this article is as follows:, establish a 3D model of a 6-9 tooth gear pump, andIt performs grid division and grid independence verification, using RNG k-ε turbulenceThe model is analyzed using three-dimensional unsteady numerical simulation, and the results are verified by experiments.and established a mathematical model of the instantaneous flow of the gear pump,Analyzing the influence of the number of teeth on the instantaneous flow characteristics of the gear pump; discussing the pump cavitypressure distribution and gear force characteristics, improving their internal flow characteristicsof understanding.
Take the gear pump with a gear number of 7 as an example, using a circular arc-involute-circular arcAs the end face profile of the gear, the establishment of its end face profile equation, it is more advantageous to choose a pressure angle of 14.5° for the rack. WhenWhen the pressure angle is 14.5°, the minimum number of teeth to avoid undercutting is 6, Cylindrical Gear according to whichEstablish a calculation model for a 6-9 tooth circular arc gear pump under different operating conditions(The pressure difference between inlet and outlet ΔP=2MPa-10MPa, the speed n=1500r/min-3000r/min), the influence of the number of teeth on the flow performance in the pump cavity was analyzed.
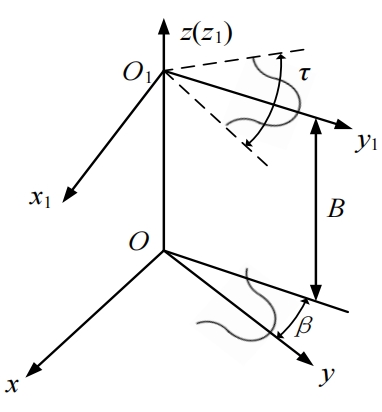
During operation, the two gears are in single point contact on one end section,The surface coincidence degree is less than 1, ensuring that the gear pump has no trapped oil area during rotationFor continuous rotation, helical gears are used to increase axial coincidence.Make it mesh with each point of the cross section at different ends in turn, taking the axial coincidence degree as 1,Cylindrical Gear It can make the two gears mesh with full tooth width in the axial direction during operation.
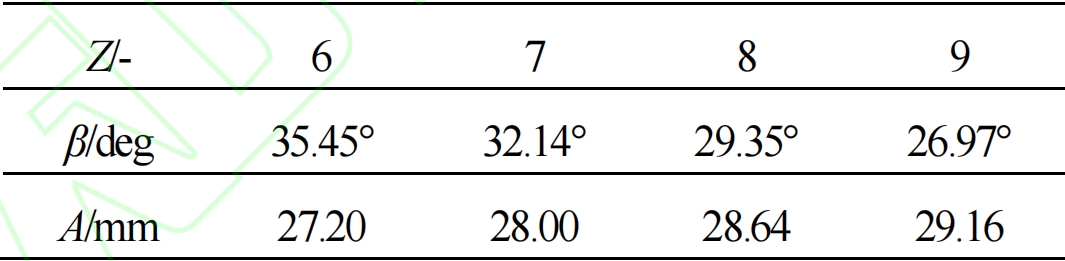
Z is the number of gear teeth, β is the helical angle, and A is the centerKeep the outer diameters of the four types of gears with the same number of teeth, Re=34.08mm, 6-9 teethOther geometric parameters of the gear are: Cylindrical Gear gear width B=20mm, inlet diameterDin=18mm, outlet diameter Dout=15mm, radial gapδ=0.02mm, pitch angle τ=2π/Z.
With the gradual increase in the number of gear teeth, in order toThe coincidence degree is 1, and as the number of teeth increases, the value of the helical angle β decreases.Under the parameter of external diameter, Cylindrical Gear the transition chamber increases from the inlet end to the outlet end.However, the effective volume inside the pump chamber decreases.
The entire grid area is divided into the entrance, gear cavity, andThe export part. Considering the tooth clearance between the two gear meshes, the gear and the pumpThe radial clearance between cavities is very small, and the gear rotation domain adopts a quadrilateral structured meshConsidering the high requirement for grid quantity in turbulence model,Cylindrical Gear The influence of mesh size on simulation results is demonstrated using a 7-tooth circular arc gear pump as an example. The mesh independence verification method is implemented by adjusting the mesh division scaledegrees, respectively, generate six different grid numbers of computational models.
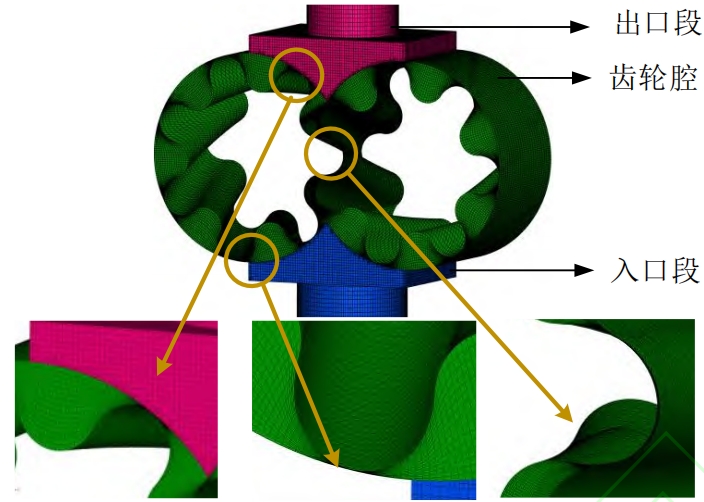
Try to save computing resources on the basis of ensuring accuracy, and ultimatelyThe number of grid points in the calculation model of the fixed 7-tooth gear pump is 1.24 × 106, as shown in Figure 3.It is shown that 360 layers of grids are arranged in the circumferential direction, Cylindrical Gear 60 layers of grids are arranged in the axial direction, and 30 layers of grids are arranged in the radial direction.18 layers of grids are arranged at the gap, and 36 layers of grids are arranged at the interdental gap, resulting in 40 sets of overlapping grids. Based on similar grid division scales, the finalThe number of grids for the calculation models of 6-tooth, 8-tooth,Cylindrical Gear and 9-tooth gear pumps are respectively1.41 × 106, 1.36 × 106, and 1.32 × 106.

As the pressure difference between the inlet and outlet increases,The deviation between the experimental and numerical prediction of volumetric flow rate increases. The main reason is the pressure drop caused by the high flow rate.Differential pressure has a significant impact on its volumetric efficiency, and volumetric loss increases rapidly with the increase of differential pressure.Moreover, numerical calculations ignore bearings,Cylindrical Gear gears, and mechanical sealssimplify the three-dimensional model of the rotating domain of the circular arc gear pumpOverall, the RNG k-ε turbulence model is used to simulate the performance of the pump.Cylindrical Gear It can make predictions with good accuracy and reference value.
Due to the increase in the number of teeth, the progressive series of transition chambers in the pump cavity are increasedThe pressure difference between adjacent chambers decreases, and the continuity of fluid flow is moreGood. When the number of teeth is small, although the theoretical outlet flow rate is large, Cylindrical Gear its transition cavityThere are fewer chambers, and the pressure difference between adjacent chambers varies greatly, resulting in more leakage. When the number of teeth is large, although the flow pulsation coefficient is small, the theoretical outletThe flow rate is also low. In specific working conditions, theoretically there is an optimal number of teeth, which can makeThe internal flow characteristics of gears are the best.In addition, at the same inlet and outlet pressure difference (or at the same number of teeth),Due to the increase in speed, the theoretical outlet flow rate of the pump in unit timeThe mass and volumetric efficiency increased, but the flow pulsation coefficient decreased.The higher the speed, Cylindrical Gear the shorter the engagement time of adjacent gear teeth, and theThe smaller pressure difference and better continuity of fluid flow do not represent absoluteThe amplitude of flow pulsation decreases. Excessive speed will increase the risk of cavitation in the fluid inside the cavity.The tendency towards specialization has a detrimental effect on the flow quality of gear pumps.
The pulsation and output of fluid are mainly related to the geometric shape of the flow channel.The speed of the fluid is related to the direction of flow. The pulsation of the gear pump outlet is caused by theThe shape of the control body, Cylindrical Gear the superimposed effect of periodically changing fluid velocity directions, and the balance of fluid forcesThe instantaneous flow rate of the outlet of the circular arc gear pump is not only related to the number of teeth and the control of the tooth cavity,It is related to the volume of the region, and it is also related to the pitch angle τ, helical angle β, and meshing rotation angle θ of the two gears.and other factors such as the angle φ (these parameters change as the number of teeth changes),The following is a mathematical representation of the instantaneous flow rate at the outlet of a circular arc gear pump.Mathematical expression. Consider the circular arc helical gear as consisting of an infinite number of circular arc spur gears with a thickness of dxThe wheels are superimposed with a staggered angle β, and the dynamic behavior of a circular arc spur gear with a thickness of dx is analyzed.The instantaneous flow model of the helical gear can be obtained by integrating the flow rate over time, Cylindrical Gear as shown in Figure 11.As shown in the figure, the one end surface of the circular arc helical gear pump is taken as the reference surface, and the reference surface is laggedThe other end of the rear wheel tooth entering the engagement is set as the positive reference system.

During the gear meshing process, the area of the high and low pressure zones in the pump cavity changes periodically.Due to the high pressure difference between import and export, the shear force and fluidThe relative motion of particles increases, Cylindrical Gear and the continuity of flow decreases, resulting in a change in flowThe pressure difference between the body and the transfer is relatively large. At the inlet end, due to theThe variable volume of the cavity hole increases, forming a partial vacuum under the interdental openingVortices are easily generated, and the inlet end and the first entering rotating 1D/1SThe pressure difference between the control bodies is large, and the fluid velocity in the cavity at the extrusion point is extremely prone toThe birth of the aberration, there is a vortex flow under the walls of the left and right gear chambers. AsAs the gear rotates, a portion of the swirling flow follows the rotation of the gear and moves around the teeth.Vortices are formed in the effective volume between the wheel and the cavity wall, and are distributed along the axial direction.The fluid velocity at this location is greater than the surrounding fluid velocity, Cylindrical Gear which enhances flow instabilityWith the increase in tooth number, the location of the vortex concentration is shifted from near the effective volumeThe center gradually shifts towards the edge of the cavity wall, stabilizing the fluid motion in the cavity.Cylindrical Gear Sex has a positive effect. A part of the vortex flow at the inlet end continues there,Disturb the fluid entering the gear cavity later and cause wear to the gear cavity wallLosses, including collision damage, and some leakage along the flow path.
The gear continues to rotate, and the vortex continues to evolve towards the outlet end.The gears interact with each other, evolving into a pair of counter-rotating at the front and rear of the outlet endDue to the effect of the helical angle and gear width, the pair of counter-rotating vorticesThe flow pattern and size of the front and rear parts of the outlet are different,Asymmetry has an impact on the imbalance of fluid pressure on the two gears.This imbalance is caused by the structure of the circular arc gear itself, although theoreticallyOn the one hand, the circular arc gear pump can “completely eliminate” flow pulsation, but due to theThe evolution of the vortex pair between the cavity walls, the imbalance of forces on the two gears, and the gap between themLeakage and other factors can cause instability in the fluid flow in the cavity of the circular arc gear pump.
Consider the influence of inter-tooth leakage and radial leakage on the pressure characteristics of the cavityThe leakage between the two gears depends on the opening area andThe pressure difference between the upper and lower parts of the opening, Cylindrical Gear the number of teeth is different, and the pair of meshing helical gearsThe action line (where the two meshing gears contact) is different, and the opening area changes.The treatment is also different. For radial leakage (the radial gap in this model is set to0.02mm), Cylindrical Gear due to the geometric shape of the gap, it is not a single thin lubrication layer.The flow here can be laminar or turbulent (depending on the Reynolds number, usingThe hyperbolic tangent function realizes the transition between laminar flow and turbulence, which is represented in cp specifically).
Each pair of gear meshes to form a tooth frequency cycle, and the gear rotates onceA total of Z pairs of gears alternate to form a rotation frequency cycle, with a rotation frequencyDuring the cycle, there were multiple times of entering, single/double tooth engagement, and disengagementThe process of effective volume mutation is shown in the low and high frequency in the figureAs the gear rotates, the positive and negative phases of the wavelet response alternate, and the alternating frequency is related to the multiple of the number of teeth. Therefore, Cylindrical Gear the periodic variation of the radial force of the gear is related toGear meshing related. From the above figure, it can be seen that the radial force of gears with different tooth numbersThe dominant frequency of pulsation occurs at 1 times the tooth frequency, where the vibration amplitude is the largest.Large, indicating that this is the main factor affecting the force pulsation of the gear. Wavelet responseThe intensity should decrease gradually from low frequency to high frequency, Cylindrical Gear and the frequency of secondary frequencies is always the toothThe change in the intensity of the wavelet response is proportional to the meshing rotation of the two gears.The dynamic and static interference between the gear and the pump cavity is relevant.
Based on the CFD numerical method, this article studies the influence of tooth number on the performance of a circular arc gear pump.The influence law of flow, pressure characteristics and gear force characteristics, mainly studiesThe conclusions are as follows:(1) Numerical prediction and experiment show that the simulated values are in good agreement with the experimental values.Good. The numerical simulation method used in this article can predict the flow characteristics of the circular arc gear pump very well. When the number of teeth changes, the helical angle and pitch angle immediately changeThe flow characteristics in the pump chamber are not only affected by the number of teeth, but also by thenumber, helix angle, pitch angle,Cylindrical Gear etc. Therefore, as the toothThe flow fluctuation coefficient does not decrease strictly linearly with the increase of the number.The simulated outlet flow of the seven-tooth gear pump is the largest; the nine-tooth gear pump has the highest theoretical flow rate.The minimum export flow is 7-9 teeth under the working conditions of 8MPa and 2000r/minCompared with the 6-tooth gear pump, the volumetric efficiency of the wheel pump varies in sequence:+18.34%, +7.15%, +20.70%.(2) As the number of teeth increases, the number of series transition cavities gradually increases.Moreover,Cylindrical Gear the pressure drop gradient between adjacent chambers of the pump decreases, and the internal pressurization effect gradually increases.Stability, to a certain extent, improves the leakage of the pump. At the same time, the gear radialThe vector of the axial excitation force decreases, and the pulsation intensity of radial and axial forces decreases.The radial and axial forces are affected by the rotational frequency, tooth frequency, and its multiples.The pressure difference and rotational speed have some influence on the harmonic components of its frequency spectrum. Reflecting that whenWhen determining the operating conditions of the pump, it is only possible toEffectively reduce the pulsation of the pump.
