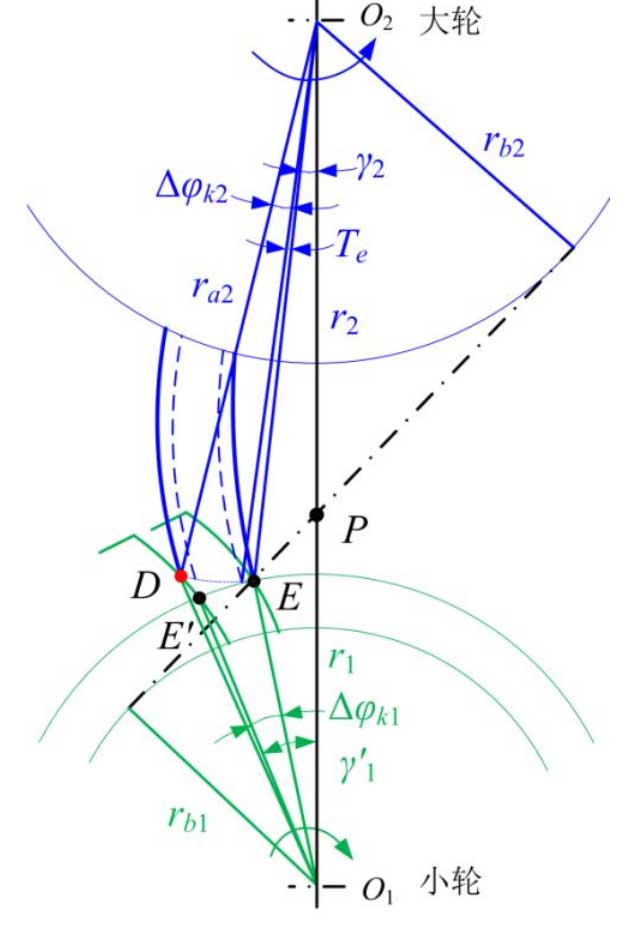
In the figure, O1 and O2 are the rotation centers of large and small wheels, point D is the actual rodent point, point E is the normal rodent point, point E’is the reversal point of the normal rodent point, and point K1 and point K2 are the reversal angles of small and large wheels in the reversal method for calculating the rodent impact point respectively, which satisfy the transmission ratio relationship.Te is LTE.
According to the engagement principle and geometric relationship, the deviation angle of the large wheel relative to the theoretical engagement position can be calculated when the engagement interference occurs.
In Figures Delta △O1DO2 and Delta △PDO2:
rO1D=a2+ra22−2ara2cos(∠PO2D) (1)
Where:
∠PO2D=γ2+Te+Δφk2 (2)
γ2=π/2−α−∠PEO2 (3)
∠PEO2=arcsinr2sin(π2+α)ra2 (4)
rO1E=a2+ra22−2ara2cosγ2 (5)
arcsin(ra2sin(∠PO2D)rO1D)−Δφk2⋅i−arcsin(ra2sin(γ2)rO1E)=inv(arccos(rb1rO1D))−inv(arccos(rb1rO1E′)) (6)
Based on the basic properties of the involute equation:
invλ=tanλ−λ (7)
The simultaneous equations (1) ~ (7) can be used to obtain the deviation angle of the large wheel from the theoretical rodent position in the case of rodent interference.
Referring to the reference data and the above formulas, the significance of each parameter is explained as follows:
Ra1 and ra2 are the top circle radius of small and large wheels respectively, R1 and R2 are the pitch radius of small and large wheels respectively, RB1 and Rb2 are the base circle radius of small and large wheels respectively, A is the center distance of engagement of two gears, I is the gear pair transmission ratio, and a is the indexing circle pressure angle.
It can be seen from the diagram that under the standard gear surface condition, when meshing interference occurs, the angle of rotation of the large wheel deviating from the theoretical meshing position is Δφk2, which is equal to Te plus k2.This angle can be superimposed on the angle at which the large wheel theory is rodented and the position vector at the impact point can be obtained by contacting the small gear tooth surface with the large wheel at a new position.
